
Cette partie présente la stratégie que nous avons suivie pour identifier un algorithme adapté à la résolution du problème de l'estimation des paramètres de COLDO étant données la non-linéarité de ce modèle (Chapitre 3) et la structure du jeu de données décrit dans le Chapitre 2. Ce quatrième chapitre est consacré à la formulation et à la caractérisation mathématique de ce problème inverse. Pour cela, nous nous placerons provisoirement dans un contexte théorique : les données in situ seront remplacées par des données artificielles non bruitées fabriquées à partir de COLDO.
D'une façon très générale, les méthodes inverses qui nous intéressent ont pour but d'estimer numériquement des caractéristiques d'un système réel à partir d'observations de ce système. La stratégie consiste à utiliser ces observations pour estimer des propriétés numériques d'un modèle, qui sont les analogues des caractéristiques naturelles auxquelles on s'intéresse (Figure 21). Cette procédure d'ajout des informations apportées par les observations à celles qui sont inclues dans les équations du modèle est appelée assimilation de données. On oppose la théorie inverse à l'approche directe (Figure 21) dont l'objet est la simulation d'un système réel avec un modèle aux propriétés connues, et à partir d'un état initial défini par des observations. La Figure 22 présente un exemple classique de problème inverse où l'on cherche à estimer la pente et l'ordonnée à l'origine de la droite - ou modèle - y(x)=a.x+b qui explique au mieux la relation entre les observations yi et les valeurs xi.
La théorie inverse a été développée dans des domaines divers, pour estimer des propriétés variées de modèles ayant des structures elles-mêmes variées… Il en résulte des formulations et des méthodes apparemment différentes selon les disciplines. En fait, la plupart des méthodes inverses reposent sur les mêmes "ingrédients de base" et c'est surtout l'interprétation de ces "ingrédients" qui varie selon les domaines. Le choix d'une méthode inverse dépend avant tout de la nature des propriétés du modèle que l'on recherche.

Figure 21. Schéma réalisé d'après Menke (1989) sur la distinction entre l'approche directe (flèches vertes) et l'approche inverse (flèches rouges).
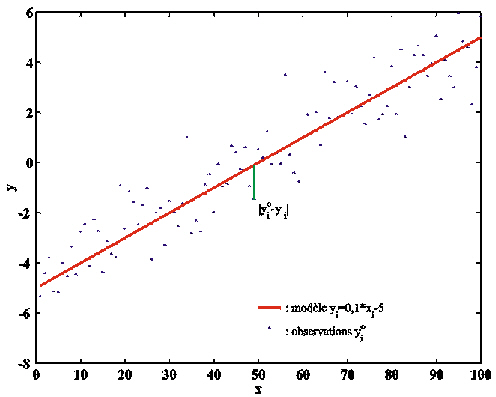
Figure 22. Un problème inverse classique: ajustement d'une droite (le “modèle”) à un ensemble d'observations. Le trait vert symbolise le calcul de la distance entre une observation yoi et la valeur prédite par le modèle, yi=a.xi +b.
En océanographie, on rencontre principalement deux grands types de problème inverse. En océanographie physique les modèles sont basés sur des lois physiques que l'on peut considérer comme exactes relativement aux lois phénoménologiques utilisées en biogéochimie. De plus, les données physiques sont beaucoup plus abondantes que les données biogéochimiques. Cependant, à cause des termes non-linéaires, des erreurs d'approximation induites par le choix des échelles représentées par les modèles et des erreurs dans la paramétrisation de ces échelles, il est nécessaire de corriger régulièrement les prévisions de l'état de l'océan pour limiter la divergence par rapport à son état réel. Pour cela, les mesures réparties dans le temps et dans l'espace sont interpolées sur la grille du modèle et comparées aux prévisions. En pondérant judicieusement l'importance des informations apportées par les mesures - par définition imprécises - et par les prévisions, une estimation améliorée de l'état de l'océan à la date considérée est réalisée, et utilisée comme condition initiale pour calculer les prévisions ultérieures. Dans ce type de problème, les propriétés du modèle que l'on recherche sont les valeurs des variables d'état à une date donnée. Plusieurs formulations de cette approche dite variationnelle sont utilisées, qui ont été initialement développées en météorologie. Elles ont ensuite été appliquées à l'océanographie physique et à la chimie atmosphérique comme le montrent les références proposées ci-dessous. Le filtre de Kalman est l'une des plus connues (De Mey, 1997; Ménard, 2000; Prinn, 2000; Todling, 2000), et possède des variantes dont le "filtre de Kalman étendu" (Evensen, 1992) et "le filtre de Kalman d'ensemble" (Evensen, 1994). On a également recours à l'interpolation optimale (De Mey, 1997), à la méthode des représenteurs (Bennett, 1992) ou à celle des fonctions de Green (Enting, 2000). Ces différentes formulations présentent de nombreuses similitudes d'un point de vue théorique (Wunsch, 1996).
L'autre type de problème inverse consiste à estimer les paramètres du modèle. On reconnaît dans cette définition le problème inverse que nous avons proposé de résoudre dans la conclusion du Chapitre 3. Pour le distinguer clairement du précédent, nous le qualifierons en accord avec Walter et Pronzato (1994) et Evensen (1998) de problème d'estimation paramétrique. C'est un problème fréquent en biogéochimie de l'océan (Vézina et Platt, 1988; Murnane, 1994; Fasham et Evans, 1995; Matear, 1995; Prunet et al., 1996b; Spitz et al., 1998; Evans, 1999; Gunson et al., 1999). En effet, il n'existe pas de loi exacte en biogéochimie. Par conséquent, les erreurs de prévision d'un modèle biogéochimique peuvent s'expliquer par une mauvaise paramétrisation (empirique) des processus, ou par un mauvais choix des valeurs des paramètres. L'estimation des paramètres permet donc dans un second temps de corriger les paramétrisations. Nous illustrerons cette application dans la section 8.2. D'autre part, comme nous l'avons mentionné plus haut, les modèles biogéochimiques sont hautement intégrés (regroupement des variables et des processus). Il est donc difficile de fixer la valeur des paramètres à partir de mesures in situ ou in vitro.
Malgré leur diversité apparente, la
majorité des méthodes inverses sont basées sur le
calcul d'une fonction coût mesurant
l'écart entre chacune des No
observations yoi et les
No simulations yi des
variables observées (Figure 22). La fonction coût,
notée J, dépend du vecteur des
propriétés du modèle que l'on recherche, soit
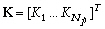 . Sa formulation la plus simple est la suivante
:
. Sa formulation la plus simple est la suivante
:
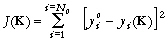 . (9)
. (9)
Dans notre cas, le vecteur K correspond au vecteur des Np = 8 paramètres du modèle COLDO, que nous noterons pnote 6.
La distance entre observations et prévisions est très généralement mesurée à partir d'une norme L2 (Eq. 9). Le choix de la norme dépend de la loi de distribution des données. Si les mesures sont supposées précises, c'est-à-dire réparties selon une distribution peu étalée, tout écart entre données et prévisions est significatif, et doit donc être fortement pénalisé. Pour cela, on choisit une norme d'ordre élevé. La norme L2 suppose que les mesures sont distribuées selon une loi gaussienne. Notons qu'en biogéochimie, la vérification de cette hypothèse exige de recourir à des tests spécifiquement adaptés à de faibles quantités de données (Madansky, 1988).
Si l'on met de côté pour le moment l'influence des erreurs sur les données, l'estimation du vecteur K expliquant le mieux les données yio revient mathématiquement à minimiser la fonction J(K). Il existe un grand nombre d'algorithmes de minimisation, dont le choix dépend en premier lieu de la forme de la fonction à minimiser. Celle-ci dépend de la dynamique - linéaire ou non-linéaire - du système étudié, du type des propriétés K - variables d'état X ou paramètres p - recherchées, et enfin de la structure du jeu de données assimilé.
La linéarité ou la non-linéarité du problème inverse dépend à la fois de la dynamique du modèlenote 7 et du type de propriété recherché. Comme le montre l'Encadré 1 sur des exemples simples, le problème inverse consistant en l'estimation des variables d'état Xi(t) d'un modèle à la date t (par exemple, à l'instant initial) est un problème inverse linéaire ou non-linéaire, selon que la dynamique du modèle est linéaire ou non-linéaire (cf. cas 1 et 2 de l'Encadré 1). Par contre, le problème de l'estimation des paramètres pi d'un modèle dynamique est toujours un problème inverse non-linéaire, que la dynamique du modèle soit linéaire ou non (cf. cas 3 de l'Encadré 1 ; Evensen et al., 1998). Dans le cas où la dynamique du modèle est non-linéaire, il s'agit d'un problème inverse fortement non-linéaire.
On en déduit que l'estimation des
huit paramètres du modèle non-linéaire COLDO
à partir des données EUMELI est un problème
inverse fortement non-linéaire.
Cas 1 : soit
le modèle dynamique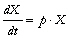 ,
,
dont la dynamique est
linéaire et dont on recherche les conditions initiales
Xo.. p est un
paramètre constant au cours du temps. La forme
discrétisée du modèle est :
où Dt est le pas de temps. En posant
Soit
yo une mesure de X à la date
tk. La fonction coût,
fonction des conditions initiales, s'écrit
:
On reconnaît
ici l'équation d'une parabole,
caractérisée par une dérivée
seconde indépendante de la variable recherchée,
Xo : Ce problème inverse est linéaire. Cas 2 : soit le modèle
dont la dynamique
est non-linéaire, et dont on recherche les conditions
initiales Xo. p est un
paramètre constant au cours du temps. La forme
discrétisée du modèle à la date
t1 est :
Soit
yo une mesure de
X1. La fonction coût Cas 3 : on considère le modèle du cas 1, dont la dynamique est linéaire. On cherche à estimer le paramètre constant p. Soit yo une mesure de X à la date tk. La fonction coût, fonction de p, s'écrit :
J(p) est
un polynôme à l'ordre 2k de
p. Ce n'est une parabole que dans la situation
où k = 1, c'est-à-dire si
l'on compare les données et les
prévisions au premier pas de temps, ce qui est peu
utile en pratique. La dérivée seconde |
Encadré 1. Démonstration dans des cas très simples de la relation entre la nature linéaire ou non-linéaire du problème inverse, la dynamique du modèle et le type de propriété estimé (variable d'état ou paramètre).
On montre que lorsque le problème inverse est linéaire et que les données assimilées permettent de contraindre toutes les inconnues Xi(t), alors toutes les sections de la fonction coût J(X(t)) le long de combinaisons linéaires des Xi(t) sont des paraboles (cf. cas 1 de l'Encadré 1 ; Figure 23a). Par conséquent, J(X(t)) n'admet qu'un minimum, qui est la solution au problème inverse. Dans le cas où le problème inverse est non-linéaire, les sections de la fonction coût le long de combinaisons linéaires des inconnues (variables d'état ou paramètres) ne sont plus des paraboles. Elles ont la forme de bols plus ou moins déformés (cf. cas 1 et 2 de l'Encadré 1 ; Figure 23a-b). Lorsque le problème est fortement non-linéaire, on montre que les fonctions coût J(p) peuvent avoir des formes très complexes, et présenter plusieurs minima locaux ainsi que des points de selle. Ces variations complexes sont l'expression des bifurcations du modèle, c'est-à-dire de la sensibilité de la dynamique des solutions vis-à-vis de la valeur des paramètres (Crawford, 1991 ; section 3.2.2).
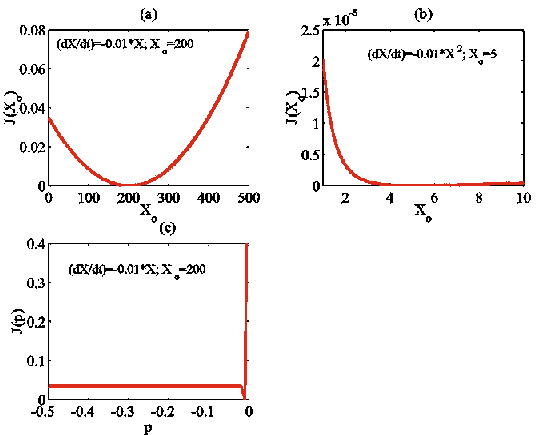
Figure 23. Forme des fonctions coût associées aux cas 1 (a), 2 (b) et 3 (c) de l'Encadré 1. La forme discrétisée des modèles est intégrée sur 500 pas de temps Dt. La comparaison entre les trajectoires d'essai et la trajectoire optimale est faite à partir de t = 10.Dt, puis tous les 10.Dt.
Nous avons étudié la complexité des fonctions coût associées à l'estimation des paramètres du modèle non-linéaire COLDO en cartographiant des sections de ces fonctions à partir de données artificielles (Athias et al., 2000a-b; Annexe 4 et Annexe 5).
Nous avons fabriqué un jeu de données artificielles représentant le transfert de l'Al au site EUMELI oligotrophe. Pour cela, nous avons intégré la version semi-spectrale du modèle (PSyDyn, section 3.2.3) pendant trois années, entre 1000 et 4200 m de profondeur, et avec un vecteur de paramètres connu popt, dont les valeurs sont données dans le Tableau 13. Elles sont comprises entre les valeurs extrêmes relevées dans la littérature (Tableau 14). Les profils initiaux du flux de masse (Fm) et du flux d'Al (Fe) ont été calculés à partir des échantillons collectés par les pièges au site O pendant la période allant du 14 au 24 mai 1991 (Bory et Newton, 2000), selon la procédure décrite dans la section 3.1.3. Le profil initial de la concentration en Al filtré (Cpe) est supposé constant avec la profondeur, et égal à la valeur mesurée par les pompes in situ en juin 1992 à 1000 m au site O (0,09963 mg/m3 ; Tachikawa et al., 1999 ; section 2.3.2(b)). Le profil initial de la concentration en Al dissous (Cde) est également supposé constant avec la profondeur. Sa valeur (0,54 mg/m3) est égale à celle mesurée à 1000 m par Gelado-Caballero et al. (1996) à proximité des Iles Canaries (28°24'N, 15°11'W) en mars 1991. Les conditions aux limites ont été calculées pour une année et sont utilisées pour chacune des trois années d'intégration. Les conditions aux limites journalières de Fm et Fe ont été calculées selon la méthode exposée dans la section 3.1.3, à partir des mesures collectées à 1000 m entre la période du 14 au 24 mai 1991 et le 6 mai 1992 au site O. Les conditions aux limites de Cpe et Cde sont constantes aux cours du temps, et égales aux valeurs des profils initiaux.
|
Symbole |
Pseudo-données des figures 24, 25 et 27 |
Pseudo-données de la figure 26 |
Source |
|
Paramètres biogéochimiques | |||
|
Kdes (/j) |
0,31940 |
0,53250 |
1 |
|
Kag (m3/mg/j) |
0,01597 |
0,01171 |
1 |
|
Kad (/j) |
0,00200 |
0,00390 |
1 |
|
Krp (/j) |
0,05090 |
0,05090 |
1 |
|
Krg (/j) |
0,05090 |
0,0509 |
1 |
|
Paramètres physiques | |||
|
Vp (m/j) |
10,00 |
10,00 |
2 |
|
Vg (m/j) |
180,00 |
180,00 |
2 |
|
Kz (m2/j) |
1000,00 |
1000,00 |
3 |
Sources : 1. cf. Tableau 14 ; 2. Whitfield et Turner (1987) ; 3. Zakardjian et Prieur (1994) ; L. Prieur, communication personnelle (1997).
Tableau 13. Valeurs des paramètres utilisées pour calculer les données artificielles associées aux cartes des figures 25 à 27.
Nous avons vérifié que ces simulations sont du même ordre de grandeur que les données réelles (Figure 24). Les simulations des Nv = 4 variables d'état ont été échantillonnées à Nd = 2 profondeurs (z1 =2000 m et z2 = 3000 m). A chaque profondeur, les valeurs ont été extraites tous les 10 jours, entre le 500ème et le 1000ème jour d'intégration, ce qui représente Nm = 51 pseudo-mesures par profondeur. Ce jeu de données artificielles contient le même type de mesures et approximativement les mêmes résolutions temporelle et spatiale que le jeu de données réelles (section 2.3.2). Nous noterons Wit (i=1,…,Nv) les (Nd´ Nm) matrices des pseudo-mesures, et Vi la variance de chaque type de pseudo-mesure. Aucun bruit n'a été ajouté aux sorties du modèle : les pseudo-données sont supposées parfaites. L'influence des erreurs des données sur la résolution du problème inverse sera abordée dans la Partie III.
Les cartes des
fonctions coût ont été
réalisées en intégrant PSyDyn avec
plusieurs vecteurs de paramètres d'essai
notés p, en utilisant les mêmes
conditions initiales et conditions aux limites que pour les
simulations de référence (Figure 24). Les
simulations obtenues ont été
échantillonnées avec la même
stratégie que pour constituer le jeu de
pseudo-données, ce qui fournit pour chaque vecteur
d'essai Nv = 4 matrices de
prévision Wi(p).
Nous avons choisi de formuler le coût selon
:
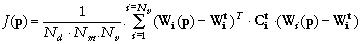
Les Nv matrices Cit sont diagonales, et leurs éléments sont les inverses des variances Vi mentionnées plus haut. Leur prise en compte rend les termes de la fonction coût adimensionnels, et permet de donner la même importance à toutes les variables d'état. Le choix de cette formulation est justifié par Athias et al. (2000a ; cf. Annexe 4 et section 5.3.1).
La Figure 25a-b montre une représentation en deux et trois dimensions d'une section de J(p). La valeur de Kad, Krp, Krg, Vp, Vg et Kz associée aux vecteurs d'essai p est égale à leur valeur optimale (Tableau 13). Les valeurs de Kdes et Kag ont été échantillonnées régulièrement dans les gammes 0-0,9369 /j et 0-0,04684 m3/mg/j respectivement, de façon à définir 2025 vecteurs p. Cette section ne couvre qu'une partie des valeurs admissibles pour ces paramètres (Tableau 14), en raison des temps de calculs élevés. Elle permet malgré tout de mettre en évidence les caractéristiques essentielles des fonctions coût associées aux problèmes inverses fortement non-linéaires (Mazzega, 2000). On constate tout d'abord que la section n'a pas la forme d'un bol. Son Minimum Global (MG) de coordonnées (0,3194 ; 0,01597) correspond aux valeurs optimales de Kdes et Kag respectivement (Tableau 13). C'est l'unique point de la section pour lequel le coût est nul. Le MG se trouve dans un large bassin d'attraction au fond très plat, dont l'axe est parallèle à celui du paramètre Kag. La section montre une autre vallée, plus étroite, dont l'axe est aussi parallèle à celui de Kag. Elle est associée à des valeurs élevées de Kdes (Kdes» 0,6 /j). Il s'agit du bassin d'attraction d'un minimum secondaire de coordonnées (0,6175 ; 0,00319) dont le coût vaut environ 38. Le point de coordonnées (0,5538 ; 0,00100) est un point de selle. A cause des instabilités numériques de PSyDyn (section 3.2.3), le coût ne peut pas être calculé pour Kdes>0,67 /j.
|
Site |
Profondeur (m) |
Traceurs |
Estimations (/an) |
Source |
|
Modèles à deux compartiments dissous et particulaire | ||||
|
Pacifique nord-ouest |
5 - 5000 |
228Th, 230Th |
Kad = 1,5 Krp = 6,3 |
1 |
|
Bassins du Guatemala et du Panama |
1000 - 4700 |
228Th, 230Th, 234Th |
0,2 £ Kad £ 1,3 1,3 £ Krp £ 6,3 |
2 |
|
Modèles à trois compartiments, identiques à ceux de COLDO | ||||
|
Mer des Sargasses |
40 - 2000 |
143Nd, 144Nd |
Kad = 4,7 ± 1,8 Krp = 127 ± 50 Kag = 55 ± 17 Kdes = 182 ± 70 |
3 |
|
Pacifique nord-ouest et Mer du Japon |
500 - 5500 |
228Th, 230Th, 234Th |
0,2 £ Kad £ 0,9 0,4 £ Krp £ 1,9 0,1 £ Kag £ 2,4 148 £ Kdes £ 3600 |
4 |
|
Station P (Pacifique Nord) |
0 - 4000 |
228Th, 230Th, 234Th |
Kad = 0,47 ± 0,09 Krp = 0,97 ± 0,09 Kag = 0,22 ± 0,01 Kdes = 0,8 ± 0,2 |
5 |
|
Pacifique Equatorial et Station P (Pacifique Nord) |
0 - 500 |
228Th, 230Th, 234Th |
Pacifique Equatorial : 1 £ Kad £ 100 0,1 £ Krp £ 73,0 0,1 £ Kag £ 55,0 14 £ Kdes £ 5500 |
6 |
|
|
|
|
Station P : 1 £ Kad £ 40 7 £ Krp £ 33 0,5 £ Kag £ 55,0 |
|
|
NABE* |
150 - 300 |
228Th, 234Th |
0,51±12 £ Kag £ 33,2±128 108±207 £ Kdes £ 407±928 |
7 |
|
Atlantique nord-ouest |
25 - 5500 |
228Th, 230Th, 234Th |
4 £ Kad £ 6 3 £ Krp £ 77 2,1 £ Kag £ 3,6 136 £ Kdes £ 196 |
8 |
|
Station P (Pacifique Nord) |
0 - 4000 |
228Th, 230Th, 234Th |
Kad = 0,74 ± 0,35 Krp = 1,7 ± 0,9 Kag = 0,3 ± 0,0 Kdes = 175 ± 3580 |
9 |
|
NABE* |
100 - 400 |
228Th, 234Th |
2,0±0,2 £ Kag £ 76±9 156±17 £ Kdes £ 524±74 |
10 |
Sources : 1. Nozaki et al. (1981) ; 2.Bacon et Anderson (1982) ; 3. C. Jeandel, communication personnelle, 1997 ; 4. Nozaki et al. (1987) ; 5. Murnane et al. (1990) ; 6. Clegg et Whitfield (1991) ; 7. Cochran et al. (1993) ; 8. Murnane et al. (Murnane et al., 1994) ; 9. Murnane (1994) ; 10. Murnane et al. (1996) ; * North Atlantic Bloom Experiment.
Tableau 14. Compilation bibliographique des estimations des paramètres biogéochimiques du cycle des particules océaniques (Athiaset al., 2000a). Ces travaux sont basés sur l'utilisation de modèles des échange dissous-particulaire similaires à COLDO, mais l'estimation des paramètres repose la plupart du temps sur l'hypothèse d'état stationnaire (cf. section 3.2.1(a)).

Figure 24. Données in situ et simulations associées au transfert de l'Al au site EUMELI oligotrophe. Les données in situ (en rouge) sont utilisées pour définir les conditions initiales et les conditions aux limites. Les paramètres utilisés pour calculer les simulations à 2000 m (trait plein bleu) et 3000 m (trait plein vert) sont donnés dans le Tableau 13. Les symboles (carrés et triangles) représentent les pseudo-mesures échantillonnées à chaque profondeur.
Ainsi, la cartographie du coût permet de retrouver les paramètres du modèle utilisés pour calculer les pseudo-données, à condition que six des huit paramètres soient fixés, c'est-à-dire supposés connus.
Nous avons réalisé la carte d'une autre section de la même fonction coût, toujours en fonction de Kdes et Kag (Figure 25c-d). Les valeurs de Krp, Krg, Vp, Vg et Kz sont toujours égales aux valeurs optimales. Mais cette fois, nous avons considéré que Kad est mal connu, et que l'on fait une erreur en fixant sa valeur à Kad = 4.10-3 /j (Tableau 13). On constate que la forme de la section est significativement différente de celle de la section précédente. Le MG a migré vers le point de coordonnées (0,4900 ; 0,00430). Son coût vaut environ 23. Le minimum secondaire s'est également déplacé vers le point de coordonnées (0,6059 ; 0,00320), dont le coût est approximativement 67. Cette expérience montre qu'une faible erreur sur la valeur d'un paramètre supposé connu peut induire une erreur importante dans le positionnement du MG.
Par conséquent, dans le cas de l'assimilation de données réelles, la fonction coût doit être minimisée simultanément par rapport aux Np = 8 paramètres de COLDO.
La Figure 26 montre une section d'une autre fonction coût, réalisée à partir d'un autre jeu de pseudo-données. Les conditions initiales, les conditions aux limites et la stratégie d'échantillonnage des simulations sont analogues à celles qui ont été décrites précédemment. Seul le vecteur des paramètres optimal est différent : il est donné dans le Tableau 13. Cette section dépend toujours de Kdes et Kag. Les six autres paramètres sont fixés à leur valeur optimale. On retrouve la présence de deux vallées, dont les axes sont parallèles à celui de Kag. Mais elles ont tendance à se rejoindre pour n'en former qu'une seule. En outre, le coût du minimum secondaire (~ 0,22), de coordonnées (0,6388 ; 0,03090) est très proche de celui du MG. Cela signifie qu'il existe deux jeux de paramètres capables de générer des pseudo-données pratiquement identiques. Cette expérience démontre que dans le cas de problèmes inverses fortement non-linéaires, les difficultés posées par la minimisation de la fonction coût dépendent du jeu de paramètres recherché.
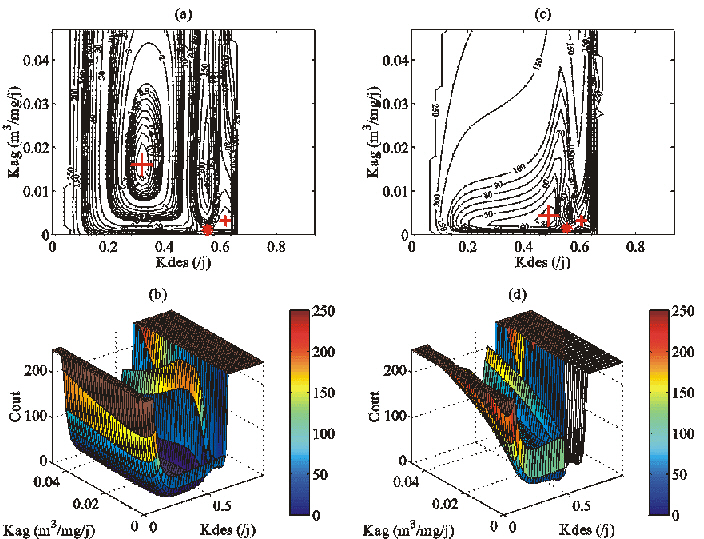
Figure 25. Sections bidimensionnelles de la fonction coût calculée avec les pseudo-données représentées sur la Figure 24. Pour la première section (a en 2D et b en 3D), les valeurs de Kad, Krp, Krg, Vp, Vget Kzsont les valeurs optimales (Tableau 13). Pour la deuxième section (c en 2D et d en 3D), la valeur de Kad est fixée à 4.10-3 /j. Les valeurs de Krp, Krg, Vp, Vget Kz sont les valeurs optimales. Les abréviations sont : MG : Minimum Global, MS : Minimum Secondaire, et PS : Point de Selle.

Figure 26. Section bidimensionnelle de la fonction coût associée aux paramètres optimaux donnés dans le Tableau 13. Les valeurs de Kad, Krp, Krg, Vp, Vget Kz sont les valeurs optimales. Les abréviations sont identiques à celles de la Figure 25.
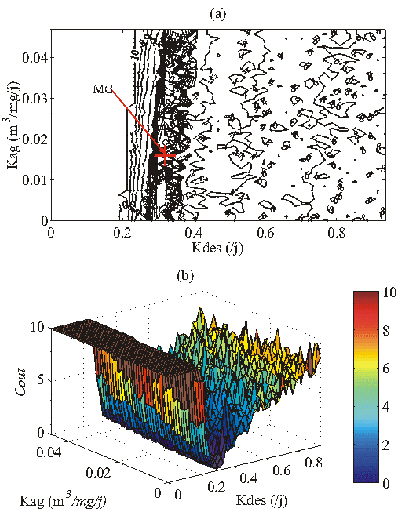
Figure 27. Section bidimensionnelle de la fonction coût associée à un jeu de pseudo-données calculées avec COLDO et les paramètres optimaux donnés dans le Tableau 13. Les valeurs de Kad, Krp, Krg, Vp, Vget Kz sont les valeurs optimales. Les abréviations sont identiques à celles de la Figure 25.
Enfin, nous avons réalisé une section d'une fonction coût associée à un jeu de pseudo-données calculé non plus avec PSyDyn, mais avec COLDO. Les paramètres optimaux, les conditions initiales, les conditions aux limites et la stratégie d'échantillonnage des simulations sont identiques à ceux utilisés pour fabriquer les pseudo-données de la Figure 24. La section obtenue en ne faisant varier que Kdes et Kag est différente de celle de la Figure 25a-b. Elle ne présente qu'une seule vallée étroite, qui est le bassin d'attraction du MG. Son axe est toujours parallèle à celui de Kag. Pour les valeurs de Kdes > 0,32 /j, la section montre un grand nombre de minima locaux. Nous pensons que ceux-ci sont liés au contrôle de la positivité des variables réalisé par COLDO (section 3.1.4) qui peut perturber la dynamique fondamentale des équations (Eqs. 2-5). Notons que COLDO peut être intégré pour des valeurs de Kdes > 0,67 /j. Cette dernière section montre que les fonctions coût associées aux deux versions du modèle possèdent le même type de complexité.
Les expériences présentées dans la suite de cette partie sont basées sur la version semi-spectrale PSyDyn, en raison de son coût réduit en temps de calcul.
éLa forme des fonctions coût, et par conséquent la possibilité de retrouver les paramètres caractéristiques d'un système réel sont largement influencées par la résolution temporelle et spatiale des données in situ, et par la nature des variables mesurées.
La dynamique non-linéaire d'un système réel est caractérisée à partir d'un ensemble d'échelles temporelles définies à partir de l'exposant de Lyapunov principal (Abarbanel et al., 1993; Abarbanel, 1996; Frede et Mazzega, 1999a-b; Mazzega, 2000 ; cf. section 3.2.2). Par exemple, l'horizon de prédiction quantifie la durée maximale pendant laquelle on peut prédire l'évolution temporelle du système. En théorie, la durée totale et la fréquence (temporelle) d'échantillonnage du système permettant de retrouver les paramètres doivent être déterminées en fonction de ces échelles temporelles. Lorsque la durée d'échantillonnage couvre plusieurs de ces échelles, les instabilités caractéristiques de la dynamique du système réel ont le temps de se manifester, et les différences entre les dynamiques associées à plusieurs vecteurs de paramètres du modèle sont détectables. Par conséquent, plus la durée sur laquelle les données in situ sont assimilées est longue, plus la résolution de la fonction coût est élevée, ce qui favorise l'individualisation des minima locaux (Mazzega, 2000). Toujours relativement aux échelles temporelles caractéristiques, l'augmentation de la fréquence d'échantillonnage revient à ajouter des points de comparaison entre les données in situ et les simulations, et permet de mieux distinguer le coût du minimum global relativement à celui des autres minima (Evensen et Fario, 1997; Mazzega, 2000). Malheureusement, les données biogéochimiques sont toujours bien trop peu nombreuses pour permettre le calcul de l'exposant de Lyapunov (Abarbanel et al., 1993). Mais la biogéochimie de l'océan est fortement influencée par les forçages physiques externes (Andersen et Prieur, 2000; Claustre et al., 2000). On peut penser que les échelles caractéristiques de ces forçages sont plus accessibles, étant donnée la relative abondance des mesures de la physique de l'océan et qu'elles contiennent des indices sur la durée et la fréquence d'échantillonnage des variables biogéochimiques (Lawson et al., 1996). Une autre approche possible pour calculer les échelles de temps caractéristiques consiste à les estimer à partir des modèles biogéochimiques, en supposant qu'ils reproduisent correctement la dynamique naturelle (Mazzega et Athias, 1998a-b).
Jusqu'à présent, aucun des articles consacrés à l'estimation de paramètres de modèles biogéochimiques ne considère l'influence de la densité (spatiale) des mesures in situ. En effet, la plupart sont basés sur l'étude de modèles à "zéro-dimension" d'écosystèmes planctoniques évoluant dans une couche mélangée supposée homogène (Fasham et Evans, 1995; Matear, 1995; Lawson et al., 1996; Spitz et al., 1998; Evans, 1999). Certains travaux utilisent des modèles décrivant l'évolution de ces écosystèmes dans une couche mélangée hétérogène verticalement, mais ils n'assimilent que des mesures (ou pseudo-mesures) de la surface de la mer. Leur objectif est de développer des méthodes d'assimilation des mesures de la couleur de l'océan (Prunet et al., 1996a-b; Gunson et al., 1999). Cependant, on peut penser qu'une augmentation de la densité des données permet de rejeter des vecteurs de paramètres générant des distributions irréalistes des variables d'état.
La nature et la diversité des types de variables observées contrôlent également la possibilité d'estimer les paramètres caractérisant le fonctionnement du système réel. Dans le cas de systèmes dynamiques non-linéaires où les variables sont très fortement couplées, l'assimilation d'observations relatives à une seule des variables d'état peut suffire à contraindre tous les paramètres (Mazzega, 2000). En effet, les couplages non-linéaires propagent les informations apportées par les observations vers toutes les variables d'état. Mais ce n'est pas toujours le cas. Par exemple, il est souvent impossible de contraindre toutes les variables d'état des modèles d'écosystèmes planctoniques par des données in situ. Matear (1995) et Prunet et al. (1996b) montrent que les données in situ dont ils disposent ne permettent d'estimer que des combinaisons linéaires des paramètres de ces modèles : ces problèmes inverses sont dits sous-déterminés. Du point de vue de la géométrie de la fonction coût, le manque d'observations indépendantes sur l'état du système réel induit une déformation du voisinage du MG. Au lieu d'avoir la forme d'un bol (dans le cas d'une section bidimensionnelle), il est étiré le long d'une vallée. On parle d'une dégénérescence de la fonction coût. C'est ce qu'on observe sur les fonctions coût calculées avec PSyDyn et COLDO (Figures 25 à 27) : l'axe du bassin d'attraction du MG est toujours parallèle à celui du paramètre Kag. En d'autres termes, les prévisions du modèle sont peu sensibles aux variations des valeurs de Kag et les mesures (ou pseudo-mesures) assimilées contraignent mal ce paramètre. Notons que dans le cas des problèmes inverses non-linéaires, l'axe de la vallée peut ne pas être rectiligne (Vallino, 2000). D'une façon générale, la sous-détermination peut être réduite en diversifiant les types d'observations.
Comme nous l'avons mentionné en comparant les figures 25a-b et 26 réalisées à partir de jeux de pseudo-données ayant la même structure (section 4.2.2(b)), la complexité de la fonction coût varie en fonction du vecteur de paramètres recherché. En effet, la dynamique du système au moment de l'échantillonnage dépend de ce vecteur de paramètres. Par conséquent, la structure du jeu de données (résolutions spatiale et temporelle, nature des variables mesurées) nécessaire pour l'estimer varie en fonction la dynamique. Autrement dit, la possibilité d'estimer les paramètres expliquant les mesures d'un système réel non-linéaire dépend de l'état du système, c'est-à-dire des paramètres eux-mêmes.
La possibilité d'estimer les paramètres caractéristiques d'un système réel dépend fortement des erreurs sur les mesures. Ce point sera étudié en détail dans la Partie III. Enfin, il est nécessaire que le modèle soit en mesure de reproduire la dynamique naturelle du système. Nous reviendrons sur cette question dans les Parties III et IV.
L'estimation des paramètres du modèle non-linéaire COLDO expliquant les données in situ collectées aux sites EUMELI est un problème inverse fortement non-linéaire. Les fonctions coût qui lui sont associées sont très complexes, et possèdent de nombreux minima locaux dans l'espace de recherche des Np = 8 paramètres.
La résolution de ce problème exige dans un premier temps de déterminer un algorithme permettant de minimiser de telles fonctions. Dans un second temps, nous devrons vérifier que la structure et la qualité du jeu de données collectées à EUMELI permet effectivement de contraindre les paramètres du modèle.
Après une présentation synthétique des stratégies employées pour résoudre les problèmes inverses linéaires, ce chapitre démontre que le formalisme et les méthodes de minimisation utilisés dans ces situations ne sont pas appliquables à l'estimation des paramètres de COLDO. Cette démonstration est illustrée par deux exemples d'application de l'approche linéaire à notre problème (Athias et al., 2000a-b).
L'analyse présentée dans le chapitre précédent montre que la résolution d'un problème inverse linéaire revient mathématiquement à minimiser une fonction coût J de Np variables dont les sections réalisées dans toutes les directions de l'espace des inconnues sont des paraboles (cf. cas 1 de l'Encadré 1 ; Figure 23a). La stratégie consiste donc à décomposer la recherche du MG du coût en plusieurs minimisations de fonctions paraboliques d'une seule variable. Ces fonctions sont des sections du coût faites dans des directions judicieusement choisies de l'espace de recherche des inconnues.
Les
algorithmes de descente de gradient sont
conçus pour minimiser des fonctions quadratiques
(Figure 28). Il s'agit donc d'algorithmes de
minimisation locale. Ils sont tous basés
sur la même stratégie. Un point de
départ K0 est choisi dans
l'espace des inconnues, puis une première
direction de progression r0 est
définie. Ensuite, l'algorithme calcule un
pas de progression
l0 adéquat dans cette
direction. La progression va toujours dans le sens de la
diminution du coût, et le point de départ
est actualisé selon :
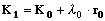
La
procédure est répétée
jusqu'à ce que l'algorithme converge
vers le minimum global du coût,
Kopt, seul point où le
gradient du coût s'annule : 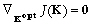 . Dans la mesure où ils reposent
sur des évaluations du gradient du coût,
ces algorithmes de minimisation sont dits
déterministes.
. Dans la mesure où ils reposent
sur des évaluations du gradient du coût,
ces algorithmes de minimisation sont dits
déterministes.
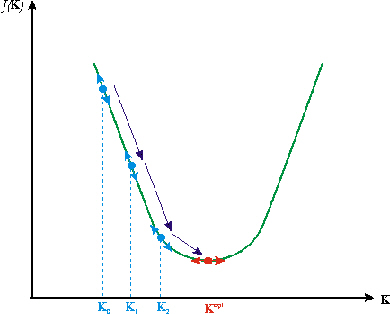
Figure 28. Minimisation par un algorithme de descente de gradient d'une fonction coût parabolique associée à un problème inverse linéaire. Kopt est la solution du problème inverse et les Kk sont les estimations successives de la solution.
Il existe
de nombreux algorithmes de descente de gradient. On
distingue en particulier la méthode de Newton,
avec ses variantes "Newton discrète", "Newton
tronquée", "quasi-Newton",
la méthode de Plus Forte Pente (PFP ou
"Steepest Descent"), et la méthode du
Gradient Conjugué (GC). Elles se distinguent
principalement par la stratégie employée
pour définir les directions de progression
successives rk. La
méthode de PFP est la plus rudimentaire de ce
point de vue. La direction rk
définie au point Kk est
celle du gradient négatif du coût. Les
méthodes de directions conjuguées
garantissent la minimisation de toute fonction
quadratique de Np variables en
Np itérations au
maximum. Les Np directions
rk (0£ k£ Np - 1)
sont linéairement indépendantes et
mutuellement conjuguées par rapport à la
forme quadratique du coût,
c'est-à-dire que :
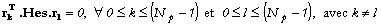
où
est Hes la matrice Hessienne du coût
:
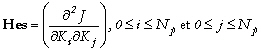 (13)
(13)
La première direction r0 est choisie de la même façon que pour la méthode de PFP. Des descriptions détaillées de ces algorithmes sont disponibles dans le recueil de Press et al. (1986) et dans celui réalisé dans le cadre du Computational Science Education Project par le Département de l'Energie des Etats-Unis (CSEP ; http://csep1.phy.ornl.gov/csep.html). Il existe également des algorithmes de minimisation locale qui ne requièrent que des évaluations ponctuelles du coût, tels que celui du simplex et celui dit de Powell (Press et al., 1986), mais ils sont peu utilisés dans notre domaine. La méthode de Powell est comparable à une méthode de directions conjuguées, mais la définition des directions rk (0£ k£ Np - 1) n'exige pas d'évaluer les dérivées de J(K) (Evans, 1999). La minimisation est terminée lorsque le scalaire lk est nul (Eq. 11).
Comme
nous l'avons mentionné
précédemment, dans beaucoup de
situations les observations
yo n'apportent pas
suffisamment d'informations pour estimer les
inconnues indépendamment les unes des
autres. Le problème inverse est
sous-déterminé. Mais il est aussi
possible que les observations contiennent des
informations trop variées pour que le
modèle puisse toutes les expliquer. Il
n'est alors pas possible de trouver de
solution au problème inverse : il est dit
sur-déterminé. En fait, la
plupart des problèmes inverses sont à
la fois sous- et sur-déterminés.
Certaines inconnues, voire combinaisons
linéaires d'inconnues, ne sont pas du
tout contraintes par les données. Elles sont
dites non-observables, et la fonction
coût montre des
dégénérescences
étirées parallèlement aux
directions définies par ces combinaisons
linéaires. Pour d'autres inconnues,
aucune valeur ne permet d'expliquer les
observations. Lorsque le problème inverse
est linéaire, nous avons montré
(cf. cas 1 de l'Encadré 1) que
les No prévisions
yi équivalentes aux
No observations
yio
dépendent linéairement du
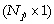 vecteur des inconnues selon
:
vecteur des inconnues selon
:

où H est une
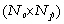 matrice correspondant au noyau
des données (Menke, 1989). A partir de
cette notation, la fonction coût de
l'équation (9) s'écrit
:
matrice correspondant au noyau
des données (Menke, 1989). A partir de
cette notation, la fonction coût de
l'équation (9) s'écrit
:
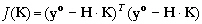
On montre que les dimensions et le rang de H, que l'on peut calculer par une décomposition en valeurs singulières, permettent d'identifier la sous- ou sur-détermination du problème (Menke, 1989; Wunsch, 1996). La décomposition de H en valeurs singulières sert aussi à repérer les combinaisons linéaires des inconnues qui sont contraintes par les observations, et à détecter les inconnues non-observables. On peut ainsi se limiter à l'estimation des seules inconnues observables. Enfin, la décomposition de H est utilisée pour déterminer les combinaisons linéaires des observations qui sont expliquées par le modèle ajusté. Cette approche algébrique revient à analyser les déformations du "bol" associé au MG (section 4.2.3).
Dans le cas où le problème inverse est faiblement non-linéaire (par opposition à fortement non-linéaire), nous avons montré que les sections du coût dans différentes directions de l'espace des inconnues ont des formes de paraboles plus ou moins déformées (cf. cas 2 et 3 de l'Encadré 1 ; Figure 23b-c). Dans cette situation, les algorithmes de descente de gradient restent généralement applicables.
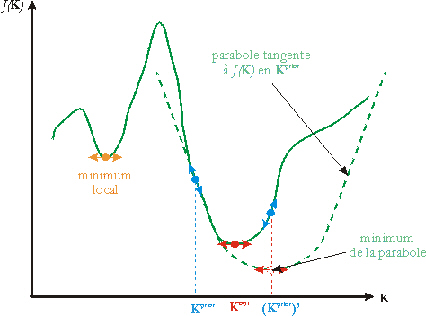
Figure 29. La linéarisation d'un problème inverse non-linéaire conduit à minimiser les paraboles tangentes à J(K) au niveau des solutions a priori calculées successivement à partir de Kprior (d'après Menke (1989)).
Dans le cas où le problème
inverse est non-linéaire, le noyau des
données H dépend des
inconnues. La relation (14) devient
:
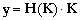
L'approche linéaire reste applicable malgré la présence de minima locaux à condition que l'on ait une bonne connaissance a priori des inconnues, c'est-à-dire que l'on soit en mesure de définir une solution a priori Kprior qui se trouve à l'intérieur du bassin d'attraction du MG. Il est alors possible de linéariser la relation (16) autour de Kprior et de se ramener localement à un problème inverse linéaire (Figure 29). La forme linéarisée est appelée modèle linéaire tangent. La minimisation par un algorithme de descente de gradient de la parabole tangente au coût en Kprior fournit une meilleure solution a priori, autour de laquelle la relation (16) est à nouveau linéarisée pour effectuer une nouvelle itération. L'itération des phases de linéarisation et de minimisation conduit progressivement au MG. Ainsi, le problème inverse non-linéaire est décomposé en une succession de problèmes inverses linéaires locaux. Mais il est important de signaler que le succès de cette approche dépend directement du choix de Kprior. Si celui-ci est défini en dehors du bassin d'attraction du MG, la minimisation conduit à un minimum local (Figure 30).
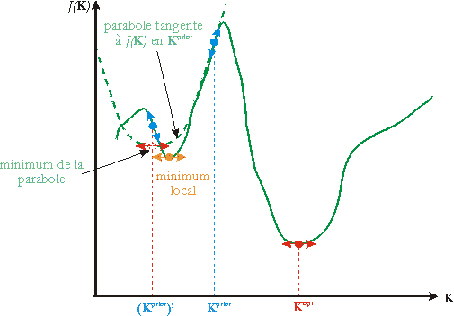
Figure 30. Dans le cas où Kprior est trop éloigné de la solution Kopt, les minimisations successives des paraboles tangentes à J(K) peuvent conduire à un minimum local (d'après Menke (1989)).
Cette formulation basée sur la linéarisation de problèmes inverses non-linéaires est fréquemment employée en océanographie. Les algorithmes de minimisation locale utilisés sont variés. Ainsi, Murnane (1994) estime les paramètres d'un modèle linéaire du cycle des particules à partir de la méthode de PFP. Les méthodes de PFP, de Newton (Lawson et al., 1996; Prunet et al., 1996b; Spitz et al., 1998; Evans, 1999; Gunson et al., 1999), celle du GC (Schartau et al., 2001) interviennent souvent dans l'estimation des paramètres de modèles d'écosystèmes planctoniques. En particulier, Spitz et al. (1998), Gunson et al. (1999) et Schartau et al. (2001) ont recours à la méthode adjointe pour estimer les gradients du coût et des paraboles tangentes (Errico, 1997). Enfin, Eknes et Evensen (1997) utilisent la méthode des représenteurs (Bennett, 1992) pour calculer certains des paramètres d'un modèle d'Ekman 1-D.
Rappelons que les problèmes inverses fortement non-linéaires correspondent à l'estimation des paramètres de modèles dont la dynamique est non-linéaire (section 4.2.2(a)). Comme nous l'avons montré dans le Chapitre 4, les fonctions coût qui leurs sont associées sont très complexes : elles possèdent de nombreux minima locaux et des points de selle. Ce sont autant de points où le gradient du coût est nul : ils vérifient donc le critère d'arrêt de la minimisation par un algorithme de descente de gradient. De plus, la sensibilité de la dynamique des modèles non-linéaires à la valeur des paramètres (section 3.2.2) ne permet pas de définir une solution a priori dont on soit sûr qu'elle se trouve dans le bassin d'attraction du MG. D'ailleurs, la largeur du bassin du MG dépend du rapport entre la durée totale d'échantillonnage et le temps caractéristique du développement des instabilités calculé à partir de l'exposant de Lyapunov principal du système (section 4.2.3). Autrement dit, ce type de problèmes inverses est non-linéarisable et l'approche inverse linéaire ne peut pas leur être appliquée. Certains auteurs l'appliquent malgré tout (Spitz et al., 1998) et pour s'affranchir de l'influence de la solution a priori sur le résultat de la minimisation, ils en essaient plusieurs et conservent le minimum dont le coût est le plus faible. Cependant, le nombre d'essais à effectuer pour trouver le MG peut être très élevé, et il doit être déterminé empiriquement.
Dans la mesure où l'on ne peut pas définir de solution a priori, on ne peut pas s'affranchir de la présence des minima locaux. Ils rendent impossible toute décomposition de la minimisation en des minimisations successives de sections. Il est donc nécessaire dans ce cas de recourir à un algorithme d'optimisation globale.
Les cartes des Figures 25a-b et 26 montrent que la forme de la fonction coût au voisinage du MG et du minimum secondaire est différente. La vallée du MG est plus large que celle du minimum secondaire. Cela signifie que la sous- ou sur-détermination du problème, et l'observabilité des paramètres, qui sont des propriétés globales du coût dans le cas linéaire, sont des propriétés locales du coût dans le cas non-linéaire. Elles ne peuvent être étudiées qu'au voisinage du MG. Cette dernière spécificité vaut pour tous les problèmes inverses non-linéaires, qu'ils soient ou non linéarisables.
Tarantola et Valette (1982) ont formalisé la résolution des problèmes inverses non-linéaires basée sur la linéarisation autour d'une solution a priori (Figure 29). Ils utilisent le critère des moindres carrés et le formalisme de l'algèbre linéaire. Cet algorithme porte le nom d'Algorithme des Moindres Carrés non-linéaire Généralisé (AMCG). C'est la technique qui a été la plus utilisée pour estimer les paramètres du cycle des particules océaniques au cours des dix dernières années (Murnane, 1994; Murnane et al., 1990, 1994, 1996).
Nous avons montré que cet algorithme n'est pas applicable à l'estimation des paramètres du modèle COLDO, en réalisant des expériences d'inversions simulées ou expériences jumelles ("twin experiments"; Athias et al., 2000a). Il s'agit de vérifier si l'algorithme de Tarantola et Valette (1982) permet de retrouver le vecteur de paramètres utilisé pour calculer un jeu de pseudo-données précis. Le jeu de pseudo-données considéré est celui que nous avons décrit dans la section 4.2.2(b), et qui est représenté sur la Figure 24. Les expériences jumelles sont très fréquemment employées pour tester des méthodes inverses (Lawson et al., 1996; Spitz et al., 1998; Gunson et al., 1999; Vallino, 2000; Schartau et al., 2001). Elles permettent en effet de s'affranchir des difficultés liées aux erreurs de paramétrisation du modèle, et des difficultés liées aux erreurs sur les données dans le cas où les pseudo-données sont supposées parfaites. Elles sont également riches en information sur la façon dont on doit interpréter les résultats d'inversions. La suite de cette seconde partie est essentiellement basée sur des expériences de ce type.
Les différentes inversions simulées réalisées avec l'AMCG correspondent à des situations variées. En particulier, certaines reposent sur l'hypothèse fréquente selon laquelle la colonne d'eau est à l'état stationnaire, et d'autres prennent en compte la variabilité temporelle des mesures. Quelles que soient les hypothèses, l'AMCG ne permet jamais de retrouver le vecteur de paramètres optimal. Nous avons montré que le formalisme fondamentalement linéaire de cet algorithme n'est pas adapté à la forte non-linéarité de notre problème inverse.
Nous avons choisi de ne pas reprendre la démonstration dans ce manuscrit. Elle est décrite dans les sections 3 et 5 de l'article d'Athias et al. (2000a) qui est reproduit dans l'Annexe 4. Dans ce même article, nous avons également montré que la formulation du coût de l'Eq. (10) est mieux adaptée à la résolution de notre problème inverse.
Nous avons également appliqué une méthode de descente de gradient à la minimisation de la fonction coût définie par l'Eq. (10). Il s'agit de la méthode du Gradient Conjugué (GC) non-linéaire : à partir d'une première solution a priori, un algorithme de GC (section 5.1) minimise des paraboles tangentes au coût de façon itérative (Figure 29). Il existe trois versions différentes du GC non-linéaire : celle de Fletcher-Reeves (Fletcher et Reeves, 1964), celle de Polak-Ribière et celle de Hertenes-Stiefel (Press et al., 1986 ; recueil du CSEP : http://csep1.phy.ornl.gov/csep.html). Nous avons choisi la première version, car c'est la plus employée. En particulier, Schartau et al. (2001) l'ont appliquée à l'estimation des paramètres d'un modèle d'écosystème planctonique. Nous avons utilisé le code développé par Gilbert et Nocedal (1992 ; http://www.ece.nwu.edu-/~rwaltz/CG+.html).
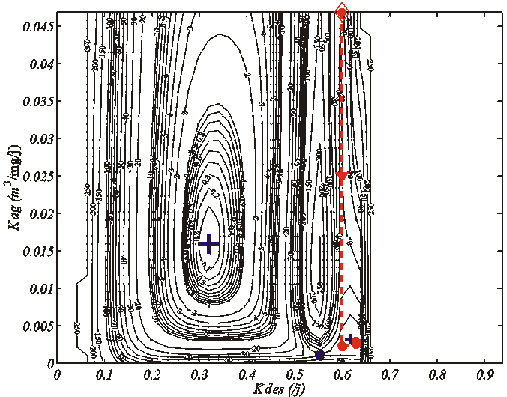
Figure 31. Minimisation de la section du coût représentée sur la Figure 25a-b par l'algorithme du gradient conjugué non-linéaire de Fletcher-Reeves (Fletcher et Reeves, 1964; Gilbert et Nocedal, 1992). Le losange rouge indique le point de départ (i.e. pprior). Les points rouges symbolisent les mises à jour des solutions a priori, autour desquelles le problème est linéarisé. La minimisation s'achève sur le minimum secondaire (petite croix bleue) de la section, et non sur le minimum global (grande croix bleue). L'étoile bleue symbolise le point de selle.
Nous avons appliqué le GC non-linéaire à l'estimation de deux (Kdes et Kag) des huit paramètres de COLDO utilisés pour calculer les pseudo-données de la Figure 24 (Athias et al., 2000b ; Annexe 5). Les six autres paramètres sont supposés parfaitement connus. Cela revient à analyser la capacité de cet algorithme à minimiser la section représentée sur la Figure 25a-b. Le point de départ, de coordonnées (0,6 ; 0,04684) se trouve à l'intérieur de la vallée secondaire. La Figure 31 montre le trajet parcouru par l'algorithme. Après 171 évaluations du coût, la minimisation s'est arrêtée sur le minimum local situé dans la même vallée que la solution a priori, c'est-à-dire sur le minimum secondaire de la section. Cette figure est une illustration du schéma théorique de la Figure 30.
Le résultat de cette expérience est indépendant de l'algorithme de descente de gradient utilisé. Le principe des méthodes de minimisation locale n'est pas adapté à l'estimation des paramètres de COLDO à partir de mesures in situ parce que la dynamique non-linéaire du modèle ne permet pas de définir de solution a priori.
Les méthodes inverses classiquement utilisées en océanographie sont basées sur une approche fondamentalement linéaire. Elles reposent toutes sur des algorithmes de minimisation locale.
La dynamique non-linéaire de COLDO rend impossible le choix de la solution a priori nécessaire pour linéariser le problème inverse associé à l'estimation des paramètres du modèle. Ce problème inverse fortement non-linéaire exige de recourir à un algorithme d'optimisation globale.
La stratégie que nous avons suivie
pour sélectionner cet algorithme fait
l'objet du chapitre suivant.
Nous avons choisi de comparer trois
Algorithmes d'Optimisation Globale
(AOG) :
- le recuit simulé est utilisé en géophysique depuis le milieu des années 1980 (Rothman, 1985) et il est régulièrement employé tant en océanographie physique (Barth et Wunsch, 1990; Krüger, 1993) que biogéochimique (Matear, 1995; Vallino, 2000) depuis le début des années 1990,
- l'algorithme génétique a la réputation d'être bien adapté aux problèmes d'estimation paramétrique (Goldberg, 1989). Il a déjà été appliqué en océanographie physique pour optimiser la stratégie de déploiement de bouées (Barth, 1992; Hernandez et al., 1995). Dans un travail contemporain du nôtre, Vallino (2000) l'a appliqué à l'assimilation de données dans un modèle d'écosystème planctonique à “ zéro dimension” ,
- le TRUST (Terminal Repeller Unconstrained Subenergy Tunneling) est encore très peu employé en géophysique. Mais d'après ses auteurs, il serait l'AOG le plus rapide (Cétin et al., 1993).
Après avoir décrit chaque algorithme, nous les comparerons sur la base d'expériences d'inversions simulées. Les premières consisteront à analyser la capacité des AOG à minimiser la section 2-D du coût représentée sur la Figure 25a-b. Notre objectif est de sélectionner celui qui fournit le meilleur compromis entre une convergence rapide vers le MG et une simplicité d'application. Le travail présenté dans ce chapitre fait l'objet d'un article (Athias et al., 2000b) qui est reproduit dans l'Annexe 5.
Le TRUST est un algorithme déterministe, c'est-à-dire basé sur l'évaluation de dérivées de la fonction à minimiser. C'est aussi un algorithme dynamique qui se déplace à vitesse variable à l'intérieur de cette fonction. Il a été développé récemment par Cétin et al. (1993) et est encore peu connu. Aussi allons-nous en rappeler succinctement le fondement mathématique : celui-ci est illustré sur la Figure 32. Des descriptions plus détaillées sont proposées par Barhen et Protopopescu (1996) et Barhen et al. (1997).
Supposons dans un premier temps
que la fonction coût à
minimiser, J, ne dépende que
d'une seule variable x dont
les valeurs peuvent varier entre
xL et
xU. Au départ,
l'une des bornes,
x*
(x* =
xL ou
xU), est
utilisée pour définir une
fonction de subénergie
notée
Esub(x,x
*), par une transformation
non-linéaire de J
:
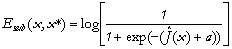
Dans cette expression,
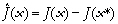 et a est une
constante. Comme le montre la Figure 32,
Esub(x,x*) a
les mêmes extrema que la fonction
à minimiser et leur ordre relatif
n'est pas modifié.
D'après
l'équation (17),
Esub(x,x*)
tend vers zéro lorsque
et a est une
constante. Comme le montre la Figure 32,
Esub(x,x*) a
les mêmes extrema que la fonction
à minimiser et leur ordre relatif
n'est pas modifié.
D'après
l'équation (17),
Esub(x,x*)
tend vers zéro lorsque 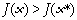 . Par conséquent,
Esub(x,x*) a
la même forme que J(x) sauf
au niveau des segments où
J(x) est supérieur à
J(x*), qui sont aplanis (Figure
32). Dans le cas où x*
n'est pas un minimum local de
J, l'exploration de
l'intervalle
[xL ,
xU] débute
par l'intégration du
système dynamique suivant
:
. Par conséquent,
Esub(x,x*) a
la même forme que J(x) sauf
au niveau des segments où
J(x) est supérieur à
J(x*), qui sont aplanis (Figure
32). Dans le cas où x*
n'est pas un minimum local de
J, l'exploration de
l'intervalle
[xL ,
xU] débute
par l'intégration du
système dynamique suivant
:
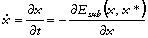
à partir du point
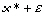 où
e est une
petite perturbation qui pousse le TRUST
à l'intérieur du
domaine de recherche. Ainsi, il descend
le gradient de
Esub(x,x*),
d'autant plus rapidement que la
pente est forte, jusqu'à
ce qu'il détecte un
minimum local. Celui-ci est à
son tour noté x* et sert
à définir une nouvelle
fonction de subénergie (Eq. 17).
Mais celle-ci est plate au voisinage de
x* (Figure 32). Cela peut aussi
se produire au début de la
minimisation, lorsque
xL ou
xU sont des
minima locaux de J. Dans ces
situations, un terme appelé
repeller est ajouté à
la fonction de subénergie, qui
éjecte l'algorithme loin
de x* :
où
e est une
petite perturbation qui pousse le TRUST
à l'intérieur du
domaine de recherche. Ainsi, il descend
le gradient de
Esub(x,x*),
d'autant plus rapidement que la
pente est forte, jusqu'à
ce qu'il détecte un
minimum local. Celui-ci est à
son tour noté x* et sert
à définir une nouvelle
fonction de subénergie (Eq. 17).
Mais celle-ci est plate au voisinage de
x* (Figure 32). Cela peut aussi
se produire au début de la
minimisation, lorsque
xL ou
xU sont des
minima locaux de J. Dans ces
situations, un terme appelé
repeller est ajouté à
la fonction de subénergie, qui
éjecte l'algorithme loin
de x* :
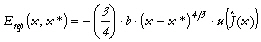
où b est la
force du repeller et u est la
fonction de Heaviside (
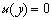 si
si 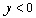 et
et  sinon).
sinon).

Figure 32. Principe de
la minimisation globale par le TRUST
suivant 4 cycles ((a) à (d);
extrait de Cétinet
al., 1993). Sur ces
schémas,
f(x)et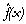 correspondent
respectivement à
J(x) et
correspondent
respectivement à
J(x) et  mentionnées
dans le texte. Le point de
départ est
x* =
xL
. Ensuite,
x1
*,
x2
* et
x3
* sont les
minima locaux détectés
successivement par le TRUST, qui sont
utilisés pour définir
les fonctions de
subénergie
Esub
(x,x*), et sur lesquels
sont définis les
“repellers”. Enfin,
xGM
* est le
minimum global.
mentionnées
dans le texte. Le point de
départ est
x* =
xL
. Ensuite,
x1
*,
x2
* et
x3
* sont les
minima locaux détectés
successivement par le TRUST, qui sont
utilisés pour définir
les fonctions de
subénergie
Esub
(x,x*), et sur lesquels
sont définis les
“repellers”. Enfin,
xGM
* est le
minimum global.
Le système
dynamique contrôlant la
progression de l'algorithme
devient :
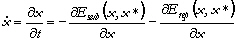
Après avoir été éjecté de x*, l'algorithme traverse le plateau qui l'entoure. Ensuite, dès qu'il rencontre une vallée il descend à nouveau le gradient de Esub(x,x*), jusqu'à ce qu'il détecte un nouveau minimum local, qui remplacera le précédent.
Ainsi, l'algorithme explore la fonction coût en alternant des phases de descente de gradient et des phases où il creuse des tunnels à l'intérieur des "monts" de cette fonction. Lorsqu'il atteint le MG, la fonction de subénergie qui est définie est constante. L'algorithme est alors éjecté du domaine de recherche (Figure 32).
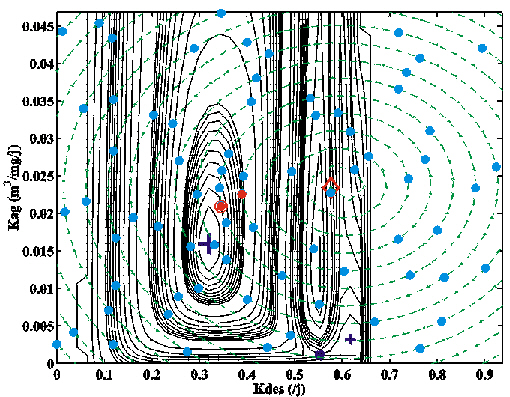
Figure 33. Première minimisation de la section bidimensionnelle du coût par le TRUST. Il minimise la fonction j(a) obtenue en échantillonnant la section par une spirale d'Archimèdès discrète (petits points et tirets verts), à partir du losange rouge de coordonnées (0,6 ; 0,02342). La fonction j(a) et le gradient des fonctions de subénergie ont été évalués sur les points bleu clair. Les points rouges sont les minima locaux détectés par le TRUST. Le dernier (encerclé) est une première estimation du MG. Le vrai MG, le minimum secondaire et le point de selle sont symbolisés respectivement par la grande croix, la petite croix et l'étoile bleues.
Cet algorithme,
conçu pour la minimisation
globale de fonctions d'une
seule variable, peut être
appliqué à la
minimisation de fonctions de
plusieurs variables, en
échantillonnant ces
fonctions par une hyperspirale
(Ammar et Cherruault, 1993). Ainsi,
pour minimiser la section 2-D du
coût (Figure 25a-b), nous
l'avons
échantillonnée par
une spirale
d'Archimèdès
discrète (Figure 33)
après avoir normalisé
le domaine de recherche de
façon à ce que les
deux paramètres varient
entre 1 et -1. On obtient
ainsi une fonction approchée
j, qui
ne dépend que de
l'angle
a. La spirale est
centrée sur le point de
coordonnées (0,6 ; 0,02342)
à l'intérieur
de la vallée secondaire. La
distance entre les spires et
l'arc entre deux points de la
spirale sont fixés
empiriquement à 0,1. La
section est couverte par 15,75
spires, dont certaines sortent
nécessairement du domaine de
recherche (Figure 33). Pour
confiner la minimisation à
ce domaine, la fonction coût
est projetée
symétriquement de part et
d'autre des
frontières. Les
systèmes dynamiques
successifs (Eqs. 18 et 20) sont
intégrés par la
méthode des
différences finies. La
constante a (Eq. 17) vaut 2
: c'est la valeur
recommandée par Cétin
et al. (1993). La force du
repeller (b, Eq. 20) a
été calculée
empiriquement de façon
à ce que l'algorithme
s'éloigne de deux pas
de spirale lorsqu'il est
éjecté d'un
repeller. L'arc
associé à la
perturbation
e est fixé
empiriquement à 0,025.
Empiriquement toujours, on estime
qu'un point est un minimum
local du coût lorsque la
norme du gradient 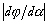 est
inférieure à
0,5.
est
inférieure à
0,5.
Le Recuit
Simulé (RS) est un
algorithme stochastique : la
minimisation repose sur des
processus aléatoires et
n'exige que des
évaluations ponctuelles de
la fonction étudiée.
Il est basé sur le
modèle thermodynamique de la
croissance des cristaux. Pour un
matériau donné, la
configuration des atomes dans un
cristal parfait correspond un
état d'énergie
minimal. Pour obtenir un tel
cristal, on peut tout d'abord
chauffer le matériau
à une température
initiale T =
To. Cet
apport d'énergie
permet le déplacement
aléatoire des atomes et le
passage à un état
liquide amorphe. Ensuite, on
diminue très progressivement
la température : c'est
la phase de recuit. Au cours du
refroidissement, les atomes
continuent à se
déplacer
aléatoirement. Toutes les
nouvelles configurations conduisant
à un diminution
d'énergie sont
réalisées. Celles qui
induisent une augmentation
d'énergie sont parfois
opérées, avec une
probabilité d'autant
plus faible que la
température est basse : elle
est proportionnelle au facteur de
Boltzman  où
DE est la
différence
d'énergie entre deux
configurations, T la
température et
kB la
constante de
Boltzman.
où
DE est la
différence
d'énergie entre deux
configurations, T la
température et
kB la
constante de
Boltzman.
Kirkpatrick et
al. (1983) ont initié
l'adaptation de ce
modèle à des
problèmes
d'optimisation globale. Le
principe du RS est illustré
sur la Figure 34. La fonction
à minimiser,
J(p), joue le
rôle de
l'énergie, et la
température est
remplacée par un
paramètre de contrôle
noté T. La
probabilité qu'une
augmentation du coût soit
acceptée est définie
à partir de la fonction de
Metropolis
fM
:
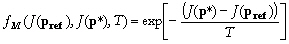
où
pref et
p* sont
respectivement l'ancien et
le nouveau vecteur de
paramètres
évalués. Le vecteur
p* est
accepté si 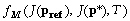 est
supérieur à un
nombre
d choisi
aléatoirement entre 0 et
1. Le RS est décrit de
façon
détaillée dans le
recueil du CSEP, par Barth et
Wunsch (1990) et Krüger
(1993).
est
supérieur à un
nombre
d choisi
aléatoirement entre 0 et
1. Le RS est décrit de
façon
détaillée dans le
recueil du CSEP, par Barth et
Wunsch (1990) et Krüger
(1993).
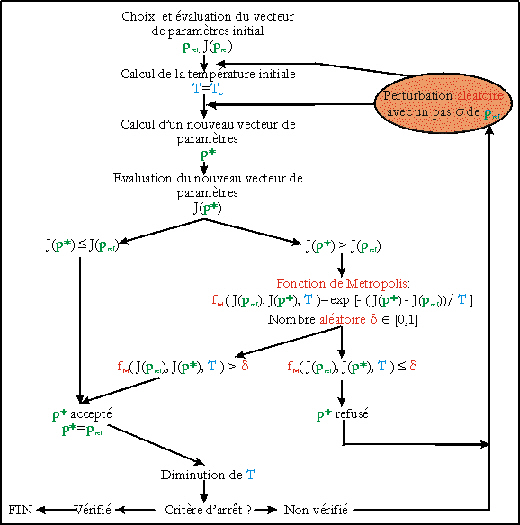
Figure 34. Principe de la minimisation de la fonction coût J(p) par le recuit simulé. Les détails sont donnés dans le texte.
Nous avons
utilisé le code disponible
sur le site internet du CSEP (http://csep1.phy.ornl.gov/csep.html). Dans un premier
temps, le domaine de recherche
est normalisé de
façon à ce que tous
les paramètres varient
entre -1 et 1. Ensuite,
huit paramètres
algorithmiques doivent être
empiriquement ajustés
(Krüger, 1993). Pour
déterminer la
température initiale
To, on
évalue le coût de
1000 vecteurs de
paramètres obtenus en
modifiant aléatoirement le
vecteur initial choisi par
l'utilisateur. On calcule
ensuite la moyenne des
augmentations du coût,
<DJ+
>, et
To est
définie selon :
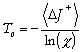
où c est la
probabilité qu'un
vecteur associé à
un coût plus
élevé que le
précédent soit
accepté. Nous
l'avons fixée
à 0,9. Le pas
aléatoire maximal que
l'algorithme peut
réaliser à partir
du vecteur de paramètres
initial,
so,
est fixé à 1. La
température T et
la longeur maximale des pas
aléatoires s diminuent par
à-coups (Figure 34).
Elles restent constantes
jusqu'à ce que 200
vecteurs de paramètres
aient été
évalués ou que
100 vecteurs aient
été
acceptés. Il
s'agit des seuils du
recuit. Ensuite, T et
s
sont réduites de 10 %.
L'exploration de la
fonction coût
s'arrête dès
qu'un seuil
vérifie les deux
critères
d'arrêt suivants
:
- aucune réduction absolue du coût n'a été enregistrée,
- la proportion des augmentations du coût acceptées relativement au nombre total des augmentations essayées doit être inférieure à 1 %.
L'Algorithme
Génétique (AG)
est également un
algorithme stochastique : il
est basé sur des
opérateurs dans
lesquels interviennent des
processus aléatoires.
Ils simulent les
mécanismes
génétiques et
ceux de la sélection
naturelle. Comme le RS,
l'AG n'exige que
des évaluations
ponctuelles de la fonction
à minimiser. Chaque
vecteur de paramètres
p est
considéré comme
le génotype d'un
individu. A partir des
limites des valeurs
réalistes de chaque
paramètre, la valeur
des paramètres est
codée en base 2 sur
une chaîne de bits. Les
séries de bits des
Np
paramètres sont mises
bout-à-bout, dans un
ordre a priori
quelconque, et le
résultat constitue le
chromosome d'un
individu haploïde. Les
simulations
générées
à partir de p
sont l'analogue de son
phénotype. Du point de
vue de notre problème
inverse, p est
d'autant plus
performant que
J(p) est
faible. On considère
donc que 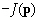 quantifie
l'adaptation de
l'individu à son
environnement (ou "fitness"). Le principe
de la minimisation est
illustré sur la Figure
35. L'AG classique
débute par la
génèse
d'une population
aléatoire
d'individus. Le
coût associé
à chacun d'eux
est évalué :
des couples de parents sont
sélectionnés
d'une façon qui
peut, selon les
méthodes, favoriser
les individus les plus
performants. Les chromosomes
des parents sont
recombinés par des
"crossovers".
Les crossovers les plus
simples correspondent
à un échange
d'une portion de la
chaîne de bits entre
les chromosomes des parents.
Ils induisent de petites
modifications des vecteurs de
paramètres dans
l'espace de recherche
et permettent
d'explorer la fonction
coût au voisinage des
individus les plus
performants. Chaque couple
donne naissance à un
ou plusieurs enfants. Les
chromosomes des enfants
peuvent à leur tour
être modifiés
par des mutations
c'est-à-dire par
des remplacements d'un
certain nombre de "0" de la chaine de bits
par des "1" et
inversement. Les mutations
favorisent les migrations de
populations entre les
vallées du coût,
c'est-à-dire une
exploration à plus
grande échelle que les
crossovers. Les enfants
deviennent à leur tour
parents. On montre que cette
manipulation des gènes
permet aux individus les plus
performants d'avoir une
descendance plus importante,
et conduit finalement au
meilleur individu. Des
descriptions
détaillées de
différents types
d'algorithmes
génétiques sont
proposées par Goldberg
(1989; 1994) et Man
(1997).
quantifie
l'adaptation de
l'individu à son
environnement (ou "fitness"). Le principe
de la minimisation est
illustré sur la Figure
35. L'AG classique
débute par la
génèse
d'une population
aléatoire
d'individus. Le
coût associé
à chacun d'eux
est évalué :
des couples de parents sont
sélectionnés
d'une façon qui
peut, selon les
méthodes, favoriser
les individus les plus
performants. Les chromosomes
des parents sont
recombinés par des
"crossovers".
Les crossovers les plus
simples correspondent
à un échange
d'une portion de la
chaîne de bits entre
les chromosomes des parents.
Ils induisent de petites
modifications des vecteurs de
paramètres dans
l'espace de recherche
et permettent
d'explorer la fonction
coût au voisinage des
individus les plus
performants. Chaque couple
donne naissance à un
ou plusieurs enfants. Les
chromosomes des enfants
peuvent à leur tour
être modifiés
par des mutations
c'est-à-dire par
des remplacements d'un
certain nombre de "0" de la chaine de bits
par des "1" et
inversement. Les mutations
favorisent les migrations de
populations entre les
vallées du coût,
c'est-à-dire une
exploration à plus
grande échelle que les
crossovers. Les enfants
deviennent à leur tour
parents. On montre que cette
manipulation des gènes
permet aux individus les plus
performants d'avoir une
descendance plus importante,
et conduit finalement au
meilleur individu. Des
descriptions
détaillées de
différents types
d'algorithmes
génétiques sont
proposées par Goldberg
(1989; 1994) et Man
(1997).
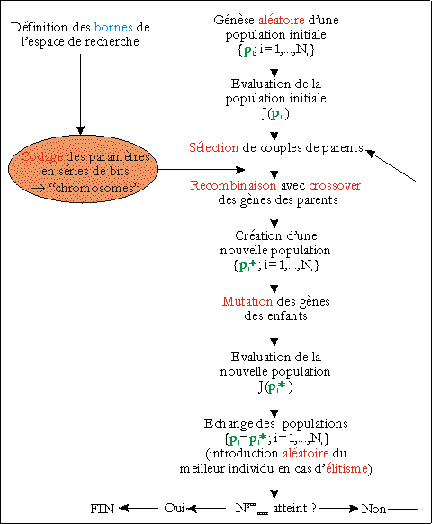
Figure 35. Principe de la minimisation par l'algorithme génétique. Les détails sont donnés dans le texte.
Nous avons
utilisé le code
développé par
Carroll (1996 ;
http://www.staff.uiuc.edu/~car-roll/ga.html).
Plusieurs versions sont
disponibles : nous avons
choisi celle que son auteur
juge la plus robuste.
L'algorithme porte le
nom de "micro-algorithme
génétique". Cette variante a
l'avantage de manipuler
de petites populations de
Ni = 5
individus, soit 20 à
40 fois plus réduites
que celles d'un AG
classique. A chaque
génération, 5
couples de parents sont
définis. Certains
individus peuvent appartenir
à plusieurs couples,
et d'autres
n'appartenir à
aucun couple. Tous les
segments des gènes
(i.e. bits de codage)
ont la même
probabilité
mc =
0,5 d'être
échangés entre
les chromosomes des parents.
Un seul enfant naît de
chaque couple, et la
probabilité que ses
gènes subissent une
mutation est nulle. A chaque
nouvelle
génération,
l'algorithme
évalue la convergence
de la population. Pour cela,
il calcule pour chaque
individu le nombre des bits
différents de ceux du
meilleur individu. Si leur
proportion est
inférieure à 5
%, cette population
disparaît. Elle est
remplacée par 4
individus
générés
aléatoirement,
auxquels s'ajoute le
meilleur individu de la
population
précédente.
Cela limite le
piégeage de
l'algorithme par un
minimum local. La
reproduction est
élitiste : le meilleur
individu est conservé
à la
génération
suivante si aucun enfant ne
l'a surpassé.
L'algorithme
s'arrête
lorsqu'il a
évalué 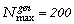 générations.
générations.
Dans un premier temps, nous allons analyser la capacité des trois AOG à retrouver les valeurs de Kdes et Kag utilisées pour calculer les pseudo-données décrites dans la section 4.2.2(b), et représentées sur la Figure 24. La précision attendue sur les estimations de Kdes et Kag est respectivement de 10-5 /j et de 10-5 m3/mg/j. Les autres paramètres du modèle sont supposés parfaitement connus ; leurs valeurs sont rappelées dans le Tableau 16. La restriction à l'estimation de ces deux paramètres permet d'étudier graphiquement le comportement des algorithmes à l'intérieur de la section du coût représentée sur la Figure 25a-b, sur laquelle nous nous sommes déjà basés pour tester l'algorithme du GC non-linéaire (section 5.3.2)
Les résultats décrits ci-dessous dépendent en partie des algorithmes choisis parmis les nombreuses variantes du RS et de l'AG (Goldberg, 1989) et des paramètres algorithmiques. Pour la plupart des paramètres algorithmiques nous avons utilisé les valeurs recommandées et nous n'avons pas cherché à les optimiser. Par contre, les résultats sont indépendants de la norme choisie pour calculer la fonction coût (Eq. 10 ; section 4.2.2(b)).
Le TRUST a trouvé le MG de la section après 2019 évaluations du coût (Tableau 15), bien que le point de départ se trouve dans le bassin d'attraction du minimum secondaire (Figure 33). Nous avons en fait réalisé six minimisations successives sur des domaines de plus en plus restreints centrés sur l'estimation du MG à la minimisation précédente. Le taux de réduction du domaine de recherche est de 70 %. La Figure 33 montre la progression du TRUST lors de la première minimisation. Rappelons qu'il minimise la fonction j(a) obtenue en échantillonnant la section à partir du centre de la spirale discrète. Les points bleu clair représentent les points où j(a) ainsi que le gradient des fonctions de subénergie successives ont été évalués. Le TRUST a détecté deux minima locaux, dont les coûts décroissent depuis le centre de la spirale. Le dernier est une première estimation du MG : ses coordonnées sont (0,3318 ; 0,02106). La fonction de subénergie associée à j(a) en ce point est plate, donc le TRUST s'est ensuite simplement déplacé vers l'extrémité de la spirale. Pour gérer les vecteurs de paramètres associés à des instabilités numériques de PSyDyn (section 4.2.2(b)), nous avons artificiellement fixé leur coût à deux fois celui du dernier repeller. Le gradient du coût en ces points vaut le double du seuil défini pour repérer les minima locaux. De cette façon, le TRUST creuse un tunnel dans les zones où PSyDyn ne peut pas être intégré.
La Figure 36a
montre
l'évolution du
coût au cours des six
minimisations. Chacune est
associée à un
nuage de points. Le
coût de
l'estimation du MG
correspond toujours au
coût le plus faible
pour chaque minimisation,
sauf pour la première.
Le point dont le coût
est inférieur à
celui de l'estimation
du GM (encerclé sur la
Figure 36a) est identifiable
sur la Figure 33 : ses
coordonnées sont
(0,3318 ; 0,01581). En fait,
la norme du gradient 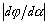 en ce
point est supérieure
au seuil de détection
des minima locaux, donc le
TRUST poursuit normalement sa
progression. A cause de la
nature discrète de la
spirale, l'algorithme
est passé par dessus
la vallée du MG
localement très
étroite.
en ce
point est supérieure
au seuil de détection
des minima locaux, donc le
TRUST poursuit normalement sa
progression. A cause de la
nature discrète de la
spirale, l'algorithme
est passé par dessus
la vallée du MG
localement très
étroite.
éLe RS a identifié le MG de la section à partir de 22 627 calculs du coût opérés sur 156 phases de recuit (Tableau 15). Les 1000 premières évaluations sont consacrées au calcul de la température initiale, soit To = 30 498. La progression du RS dans la section est représentée sur la Figure 37.
Nous avons fait débuter le RS dans la vallée secondaire, sur le même point de départ que l'algorithme du GC non-linéaire (Figure 31). Il a exploré la totalité du domaine de recherche, avant de se concentrer dans le bassin d'attraction du MG, et n'a pas été piégé par le minimum secondaire. Une analyse attentive des résultats montre qu'un grand nombre d'évaluations sont redondantes. Lorsque la modification aléatoire du dernier vecteur évalué conduit le RS à un vecteur avec lequel PSyDyn est instable numériquement, ce dernier est refusé, et l'algorithme doit faire un nouvel essai. Si elle conduit à un vecteur situé au-delà des limites du domaine exploré, l'algorithme est ramené à l'endroit où la limite a été franchie. La Figure 37 montre que cette technique tend à faire stagner l'algorithme sur les frontières du domaine.
La Figure 36b montre l'évolution du coût au cours de la minimisation. Globalement, le coût diminue progressivement. On observe clairement que le RS accepte des augmentations du coût, mais avec une fréquence qui diminue avec la température. On constate également que le coût du dernier vecteur de paramètres évalué à la fin d'un seuil de recuit n'est pas forcément le plus faible. Cela s'explique par les critères qui contrôlent le passage d'un seuil à un autre (section 6.1.2). Entre le 50ème et le 65ème seuil, tous les coûts sont très proches. A ce moment, le RS explore la région centrée autour de (0,3 ; 0,027) où le gradient est très faible (Figure 37). Le MG est trouvé dès le 90ème seuil : le premier critère d'arrêt de l'algorithme est vérifié. L'algorithme oscille ensuite autour de la solution, jusqu'à ce que la proportion des augmentations du coût acceptées soit inférieure à 1 % (deuxième critère d'arrêt).
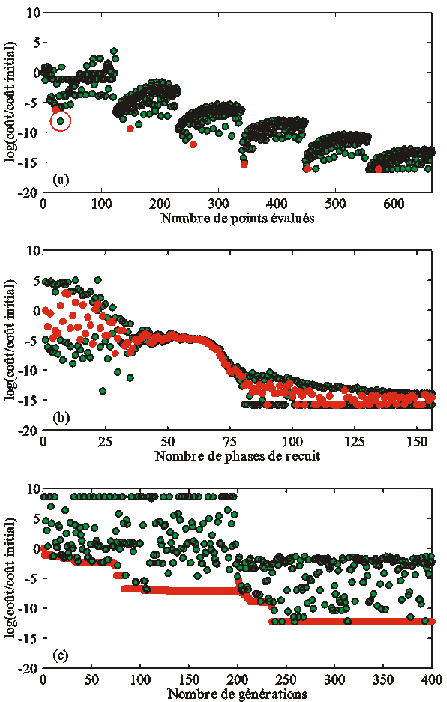
Figure 36. Evolution du coût au cours de l'estimation de Kdes et Kag (a) par le TRUST: le coût des vecteurs évalués est représenté par les points verts. Les six points rouges sont les estimations du MG calculées au cours de six minimisations successives. Le point vert encerclé montre que l'estimation de la première minimisation n'est pas optimale; (b) par le recuit simulé: les points rouges représentent le coût du dernier vecteur accepté à la fin de chaque seuil de recuit. Les points verts symbolisent les coûts les plus faibles et les plus élevés pour chaque seuil; (c) par l'algorithme génétique: les points rouges et verts indiquent respectivement le coût des individus les plus et les moins performants de chaque génération.
Pour tester la robustesse du RS relativement au point de départ, nous avons réalisé deux autres minimisations, avec les mêmes paramètres algorithmiques. Elles débutent aux coins de coordonnées (0 ; 0) et (0 ; 0,04684). Les température de départ sont similaires à la précédente (To = 30 285 et To = 30 274 respectivement). Le RS retrouve le MG dans les deux cas, après 18 293 et 22 721 calculs du coût respectivement. Par contre, nous avons constaté que le RS peut être piégé par un minimum local si le point de départ est situé à l'intérieur du domaine de recherche.
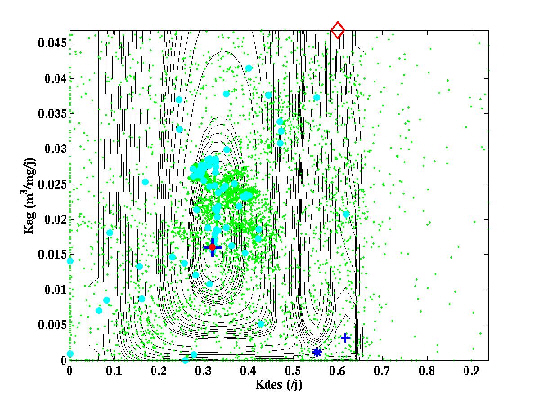
Figure 37. Minimisation de la section bidimensionnelle du coût par le recuit simulé. Le losange rouge symbolise le point de départ de coordonnées (0,6; 0,04684). Les petits points verts sont les 21 627 vecteurs évalués. Les points bleus sont les derniers vecteurs évalués à la fin de chacun des 156 seuils de recuit. La minimisation s'est arrêtée sur le point rouge. Le MG, le minimum secondaire et le point de selle sont symbolisés respectivement par la grande croix, la petite croix et l'étoile bleues.
L'AG a trouvé le MG en réalisant 2000 calculs de la fonction coût (Tableau 15). Comme pour le TRUST, nous avons réalisé deux minimisations successives, au cours desquelles 200 générations de 5 individus ont été évaluées. La Figure 38 montre le comportement de l'AG au cours de la première minimisation. Les individus de la première génération sont très dispersés. L'un d'eux est situé dans le bassin d'attraction du minimum secondaire. Malgré cela, l'algorithme n'a pas été piégé par ce minimum local. Il a exploré toutes les régions, même celles où PSyDyn est instable. En effet, lorsqu'un individu (i.e. vecteur de paramètres) susceptible de générer des instabilités est détecté, on lui affecte artificiellement une mauvaise adaptation à son milieu (i.e. un coût égal à 10 000), de façon à réduire au maximum sa descendance. Dans la mesure où les bornes du domaine servent au codage des paramètres en binaire, aucun individu ne peut naître en-dehors de celui-ci. La convergence de l'AG vers le voisinage du MG est très rapide, ce qui explique que tous les meilleurs individus ne sont pas observables sur la Figure 38. La première estimation est très proche de la solution : c'est le point de coordonnées (0,3207 ; 0,01612).
|
|
TRUST |
Recuit Simulé |
Algorithme Génétique |
|
Optimisation de Kdes et Kag | |||
|
Nombre d'évaluations du coût |
2 019 |
22 627 |
2 000 |
|
Coût maximal évalué |
3 278,3192 |
9 917,5037 |
7 571,6474 |
|
Coût final |
0,0000 |
0,0000 |
0,0000 |
|
Optimisation des Np = 8 paramètres du modèle | |||
|
Nombre d'évaluations du coût |
- |
17 244 |
1 000 |
|
Coût maximal évalué |
- |
9 970,4787 |
8 111,3732 |
|
Coût final |
- |
94,7349 |
1,3092 |
Tableau 15. Résultats des expériences d'inversions simulées. On rappelle que les pseudo-données fabriquées à partir du modèle sont non bruitées.
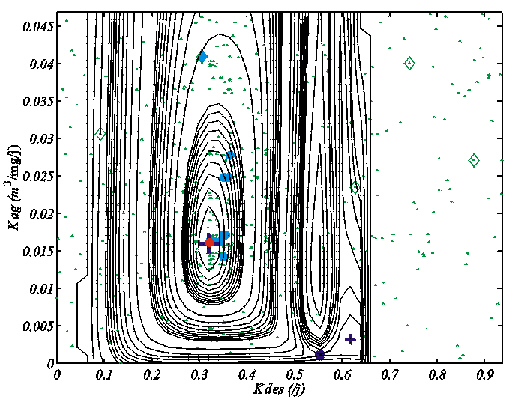
Figure 38. Première minimisation de la section bidimensionnelle du coût par l'algorithme génétique. L'algorithme a évalué 1000 vecteurs de paramètres (petits points verts). La première génération de 5 individus est indiquée par les losanges verts. Les points bleus représentent les meilleurs individus de chacune des 200 générations. Le point rouge est la première estimation du MG. Le MG, le minimum secondaire et le point de selle sont symbolisés respectivement par la grande croix, la petite croix et l'étoile bleues.
La Figure 36c représente l'évolution du coût des individus les plus et les moins performants de chaque génération au cours des deux minimisations. On constate que le meilleur individu reste identique entre la 129ème et la 200ème génération : cela reflète la nature élitiste de la reproduction. La seconde minimisation a été réalisée sur un domaine centré sur la première estimation, et contracté de 90 et 98 % dans la direction de Kdes et Kag respectivement. Le choix de ce domaine est explicité par Athias et al. (2000b ; Annexe 5). Nous ne reviendrons pas sur ce point, car nous pourrons toujours nous contenter de minimisations sur 200 générations pour les inversions ultérieures. Le coût diminue très lentement à partir de la 240ème génération, et le MG est détecté à la 368ème génération.
Il nous est rapidement apparu que la complexité du TRUST rend son application à l'estimation de plus de deux paramètres très laborieuse. Nous justifierons ce point en détail dans la section 6.3. Par contre, si l'on fait abstraction des éventuelles limitations liées au temps de calcul, l'estimation des huit paramètres du modèle par le RS ou l'AG ne pose pas plus de difficulté que celle de deux paramètres. Les deux inversions simulées suivantes comparent donc la capacité de ces deux algorithmes à retrouver les huit paramètres utilisés pour calculer les pseudo-données (Tableau 16). Les paramètres algorithmiques sont inchangés. Les intervalles de recherche des paramètres sont définis à partir des valeurs trouvées dans la littérature (Tableau 16).
|
Symbole |
Valeur optimale (popt) |
Intervalle de recherche |
Source |
|
Paramètres biogéochimiques | |||
|
Kdes (/j) |
0,31940 |
[0 ; 2,2] |
1 |
|
Kag (m3/mg/j) |
0,01597 |
[0 ; 0,22] |
1 |
|
Kad (/j) |
0,00200 |
[0 ; 0,0137] |
1 |
|
Krp (/j) |
0,05090 |
[0 ; 0,356] |
1 |
|
Krg (/j) |
0,05090 |
[0 ; 0,356] |
1 |
|
Paramètres physiques | |||
|
Vp (m/j) |
10,00 |
[0 ; 10] |
2 |
|
Vg (m/j) |
180,00 |
[0 ; 200] |
2 |
|
Kz (m2/j) |
1000,00 |
[25 ; 2000] |
3 |
Sources : 1. cf. Tableau 14 ; 2. Whitfield et Turner (1987) ; 3. Zakardjian et Prieur (1994) ; L. Prieur, communication personnelle (1997).
Tableau 16. Délimitation des intervalles de recherche des huit paramètres du modèle à partir d'une compilation bibliographique.
La minimisation par le RS a été initiée avec un vecteur dont les composantes sont les valeurs minimales des paramètres. Le calcul de la température fournit To = 64 497. Le coût a lentement décru de ~395,78 à ~94,73 et l'algorithme s'est arrêté après 16 244 évaluations du coût réalisées sur 144 phases de recuit (Tableau 15). La Figure 39a montre que dès la 70ème génération, il s'est trouvé piégé dans le bassin d'attraction d'un minimum local. Il est possible que nous aurions trouvé la solution en ajustant les paramètres algorithmiques, mais ce n'était pas notre objectif : nous recherchons un algorithme robuste.
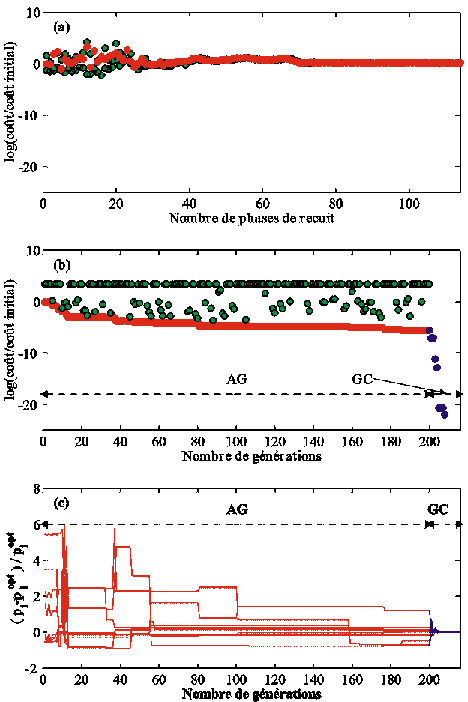
Figure 39. Estimation des huit paramètres du modèle utilisés pour calculer les pseudo-données décrites dans la section 4.2.2(b). (a) Evolution du coût pendant la minimisation par le recuit simulé. Pour chaque seuil de recuit, les points verts représentent les coûts extrêmes, et les points rouges le dernier coût évalué à la fin du seuil. (b) Evolution du coût lors de la minimisation par l'algorithme génétique sur 200 générations, puis par l'algorithme du gradient conjugué non-linéaire sur 16 itérations. Les points rouges et verts correspondent respectivement aux individus les plus et les moins performants de chaque génération. (c) Estimation des paramètres par l'algorithme génétique couplé à l'algorithme du gradient conjugué non-linéaire. Pour chaque paramètre, la différence entre la valeur estimée (p i) et la valeur optimale (p iopt ) est normalisée relativement à la valeur optimale.
L'évaluation de 200 générations par l'AG (soit 1000 évaluations du coût) a permis de rapidement localiser un vecteur dans le voisinage du MG dont le coût est ~1,31 (Tableau 15 ; Figure 39b-c). Nous avons constaté lors de l'estimation de Kdes et Kag que la convergence de l'AG dans le proche voisinage du MG est très lente. Par conséquent, au lieu de poursuivre la minimisation avec l'AG, nous avons amorcé une descente de gradient avec de l'algorithme du GC non-linéaire utilisé dans la section 5.3.2 (Gilbert et Nocedal, 1992) à partir de l'estimation calculée par l'AG. Le MG a été détecté après 741 calculs du coût supplémentaires, ce qui confirme que l'AG a bien détecté le bassin d'attraction de la solution. Pour comparaison, la poursuite de la minimisation par l'AG conduit à un coût de ~0,66 après 7250 calculs supplémentaires du coût.
Les
expériences
décrites dans la
section 6.2 montrent que les
trois AOG permettent de
retrouver les valeurs de
Kdes et
Kag
utilisées pour
calculer les
pseudo-données non
bruitées (Tableau 15).
Contrairement à ce que
l'on aurait pu attendre
d'algorithmes de
minimisation locale, ils
n'ont pas
été
piégés par le
minimum local de la section,
bien que nous les ayions fait
débuter à
l'intérieur de
la vallée secondaire.
Ils n'ont pas non plus
été
piégés par le
point de selle, et ils ont
convergé malgré
le faible gradient du
coût dans le bassin
d'attraction du MG.
Cette section présente
une comparaison du
comportement des trois
algorithmes dans le but
d'en sélection
un. Nous nous sommes
basés sur des
critères d'ordre
très
général de
façon à pouvoir
à terme appliquer
cette approche à
d'autres modèles
biogéochimiques
:
- Les modèles biogéochimiques sont caractérisés par un grand nombre de paramètres - plusieurs dizaines généralement -. Le coût de l'algorithme, en terme d'effort de programmation et de temps de calcul, doit être compatible avec le nombre élevé des paramètres.
- Les paramètres des modèles biogéochimiques sont soumis à une contrainte de positivité. Plus généralement, les domaines de recherche des paramètres sont bornés : l'algorithme doit permettre un gestion aisée des frontières.
- L'algorithme doit être robuste si l'on veut généraliser son application à différents modèles biogéochimiques tout en s'affranchissant d'une phase d'ajustement laborieuse.
Il peut apparaître in fine que nous aurions pu anticiper certains défauts des algorithmes. En fait, leurs avantages et inconvénients interagissent fortement et d'une façon qui dépend du problème. Les tester sur des inversions simulées était donc une étape essentielle, qui nous a permis en outre de progresser dans la compréhension du problème inverse.
La minimisation de la section bidimensionnelle par le TRUST est approximativement aussi coûteuse en terme de temps de calcul que celle faite par l'AG (Tableau 15). Mais le TRUST s'avère être très mal adapté au problème inverse que nous étudions.
Son
défaut majeur
provient de sa nature
déterministe : sa
convergence dépend
directement de
l'évaluation
des dérivées
de
j(a). La
dérivée
première intervient
dans les phases de descente
de gradient (Eqs. 18 et 20
; Figure 32). Nous avons
montré (Figures 33
et 36) que le
résultat de la
minimisation est
influencé par le
choix du seuil de
détection des minima
locaux, dont la valeur doit
être ajustée
à la structure de la
fonction à
minimiser. En outre, nous
avons calculé les
gradients de j(a)
par la méthode des
différences finies.
Nous pensons que cette
méthode
grossière devient
rapidement insuffisante
dans le cas de fonctions
très
irrégulières,
telles que celle de la
Figure 28. Celle-ci a
été
calculée à
partir de la version non
spectrale du modèle,
que nous comptons utiliser
pour l'assimilation
des données
réelles. Le calcul
des gradients exige alors
de recourir à des
méthodes plus
précises, mais aussi
beaucoup plus lourdes
à programmer, telle
que la méthode
adjointe (Spitz et
al., 1998; Gunson et
al., 1999; Schartau
et al., 2001). Cela
risque de rendre la
programmation de la
minimisation très
laborieuse. De plus, la
force du repeller b
(Eq. 20) dépend en
toute rigueur de la
dérivée
seconde 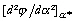 au niveau
des repellers a*.
Nous avons simplifié
l'algorithme de
Cétin et al.
(1993) en supposant que
b est une constante,
mais la validité de
cette approximation est
vraisemblablement
dépendante du
problème
considéré.
au niveau
des repellers a*.
Nous avons simplifié
l'algorithme de
Cétin et al.
(1993) en supposant que
b est une constante,
mais la validité de
cette approximation est
vraisemblablement
dépendante du
problème
considéré.
Dans la mesure où les fonctions coût associées à l'estimation des paramètres des modèles biogéochimiques - très généralement non-linéaires - sont très complexes, et que nous n'avons pas directement accès à leurs dérivées, nous pensons que les méthodes déterministes sont d'une façon générale mal adaptées à ce type de problèmes inverses. En testant plusieurs méthodes inverses sur l'estimation des paramètres d'un modèle d'écosystème planctonique, Vallino (2000) aboutit à la même conclusion.
Si la convergence du TRUST original est rigoureusement démontrée dans le cas de la minimisation de fonctions continues d'une seule variable (Cétin et al., 1993), celle de notre version simplifiée appliquée à l'estimation de plusieurs paramètres n'est pas garantie. Rappelons que la plupart des paramètres algorithmiques ont dû être ajustés empiriquement, tels que ceux qui sont associés à la résolution d'échantillonnage de la spirale d'Archimèdès, b (Eq. 20) et e. Or ils dépendent étroitement de la structure de la fonction coût.
Plus généralement, l'application du TRUST à des problèmes concrets se révèle être très laborieuse. C'est un algorithme récent, dont aucun code n'est directement disponible dans la littérature ou sur internet. L'échantillonnage des fonctions de plusieurs variables par une hyperspirale (Ammar et Cherruault, 1993) pour se ramener à une fonction d'une seule variable devient vite délicat lorsque le nombre de variables augmente. En outre, la géométrie de la spirale rend très difficile la prise en compte des bornes du domaine de recherche. La projection de la fonction coût de part et d'autre des frontières devient également très complexe lorsque la dimension du problème augmente. Ces difficultés justifient que ne n'ayions pas testé le TRUST sur l'estimation des huit paramètres du modèle. Le TRUST est donc très mal adapté à l'estimation des nombreux paramètres des modèles biogéochimiques.
En conclusion, si le TRUST est un algorithme très séduisant d'un point de vue théorique, il est extrêmement délicat à appliquer. Cela expliquerait son utilisation encore très limitée à l'heure actuelle.
A la différence du TRUST, le RS et l'AG sont des algorithmes stochastiques qui n'exigent que des évaluations ponctuelles des fonctions coût. Leurs bases conceptuelles sont telles que leur application n'est pas compliquée par l'augmentation du nombre de paramètres à estimer. D'une façon générale, les méthodes stochastiques sont mieux adaptées à l'estimation des paramètres des modèles biogéochimiques. Il faut noter cependant que leur convergence n'est que statistique et que, comme pour le TRUST, elle ne peut pas être rigoureusement garantie.
Le RS est appliqué depuis suffisamment longtemps pour que des codes soient directement disponibles dans la littérature ou sur internet. Le test de la minimisation de la section 2-D montre que s'il trouve le bassin d'attraction du MG, le RS est ensuite capable de localiser très précisémment le MG, même si le gradient local est faible. La technique mise en place pour limiter l'influence des instabilités numériques de PSyDyn semble efficace, dans la mesure où le RS se concentre rapidement vers les régions où le modèle est intégrable.
Cependant, le RS possède un certain nombre de lacunes. Tout d'abord, il est extrêmement coûteux : la minimisation de la section 2-D exige dix fois plus de calculs du coût que le TRUST ou l'AG (Tableau 15). Le temps de calcul pourrait peut-être être réduit en optimisant certains paramètres algorithmiques, mais certainement pas de façon significative car il est lié à la nature purement stochastique de l'algorithme. Aucune information sur les vecteurs déjà évalués n'est mémorisée, ce qui rend possible les redondances. Seule la diminution de la température (T) et du pas maximal de déplacement aléatoire (s) favorise statistiquement la convergence vers le MG (Figure 34). Ce défaut limite considérablement son application à l'estimation d'un grand nombre de paramètres. D'autre part, nous avons testé plusieurs méthodes pour maintenir le RS à l'intérieur du domaine de recherche, et aucune n'est réellement satisfaisante. Celle que nous avons choisie induit la stagnation du RS sur les frontières du domaine (Figure 37).
Enfin, le RS est un algorithme peu robuste. Le nombre de paramètres algorithmiques à ajuster est très élevé (section 6.1.2). Nous n'avons pas trouvé de règle - même empirique - qui permettrait de fixer objectivement leur valeur en fonction du problème à résoudre. Par exemple, la convergence dépend très fortement du schéma de décroissance de la température (Krüger, 1993). Or il existe un grand nombre de procédures empiriques pour fixer To qui produisent des résultats très variables. Nous avons pu constater en les testant qu'elles ne permettent pas toutes au RS de converger. Bien qu'il soit stochastique, sa convergence dépend du point de départ : comme le signalent les auteurs du recueil du CSEP ( http://csep1.phy.ornl.gov/csep.html) il vaut mieux choisir un point de départ situé sur la frontière du domaine exploré. Le fait que le RS ait été piégé par un minimum local lors de l'estimation des huit paramètres du modèle confirme son manque de robustesse.
Bien que son usage soit encore peu répandu, l'AG originel est très simple à appliquer. Si l'intérêt croissant pour les algorithmes basés sur les théories de l'évolution des espèces (globalement qualifiés d'algorithmes évolutifs ; Bäck, 1992, 1996; Bäck et Schwefel, 1993, 1996; Schoenauer et Michalewicz, 1997) conduit à un raffinement et à une complexité croissante, on trouve dans la littérature (Goldberg, 1989, 1994) et sur internet (Carroll, 1996, 1997) des versions simples et efficaces.

Figure 40. Cube associé à un schème de dimension 3. Le schème **0 désigne la base du cube (d'après Manet al., 1997).
L'AG
peut en fait être
qualifié de "
quasi-stochastique"
, ce qui lui confère
trois avantages essentiels
par rapport au RS. Tout
d'abord, le fondement
de la théorie des AG
repose sur la manipulation
de schèmes.
Un schème 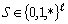 est une
description d'un
hyperplan dans un espace
à
est une
description d'un
hyperplan dans un espace
à 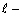 dimensions
(Man et al., 1997).
Prenons l'exemple
d'un domaine de
recherche pouvant
être codé sur
trois bits. Il peut
être
représenté
par un cube dont la
chaîne 000 est
l'origine (Figure
40). Si l'on associe
le symbole ‘*'
au cas où la valeur
du bit (0 ou 1) n'a
pas d'importance,
alors le schème **0
désigne la base du
cube. Ainsi, la chaine de
bits issue du codage
d'un vecteur de
paramètres
correspond à la
juxtaposition de
schèmes. Cela
signifie que lorsque
l'AG évalue ce
vecteur, il n'en
retire pas qu'une
information sur la valeur
ponctuelle du coût :
il en extrait une
information sur les
performances de plusieurs
hyperplans impliqués
dans la
géométrie de
la fonction coût.
L'évaluation
d'une population de
vecteurs apporte donc une
information statistique sur
la géométrie
de la fonction coût.
La théorie des
schèmes est à
la base de
l'hypothèse
des briques
élémentaires
("building block
hypothesis" ).
Les “ briques”
désignent des
schèmes de faible
dimension, d'ordre
faible
(c'est-à-dire
dont beaucoup de positions
peuvent être
désignées par
le symbole ‘*')
et très performants.
Selon cette
hypothèse,
l'AG recherche le MG
en juxtaposant les briques
qu'il a
identifiées et
mémorisées au
cours du run.
L'accès
à une information
statistique sur la forme du
coût, et la
mémorisation
partielle de cette
information par les
mécanismes
génétiques
expliquent la
réduction du temps
de calcul entre le RS et
l'AG (Figure
14).
dimensions
(Man et al., 1997).
Prenons l'exemple
d'un domaine de
recherche pouvant
être codé sur
trois bits. Il peut
être
représenté
par un cube dont la
chaîne 000 est
l'origine (Figure
40). Si l'on associe
le symbole ‘*'
au cas où la valeur
du bit (0 ou 1) n'a
pas d'importance,
alors le schème **0
désigne la base du
cube. Ainsi, la chaine de
bits issue du codage
d'un vecteur de
paramètres
correspond à la
juxtaposition de
schèmes. Cela
signifie que lorsque
l'AG évalue ce
vecteur, il n'en
retire pas qu'une
information sur la valeur
ponctuelle du coût :
il en extrait une
information sur les
performances de plusieurs
hyperplans impliqués
dans la
géométrie de
la fonction coût.
L'évaluation
d'une population de
vecteurs apporte donc une
information statistique sur
la géométrie
de la fonction coût.
La théorie des
schèmes est à
la base de
l'hypothèse
des briques
élémentaires
("building block
hypothesis" ).
Les “ briques”
désignent des
schèmes de faible
dimension, d'ordre
faible
(c'est-à-dire
dont beaucoup de positions
peuvent être
désignées par
le symbole ‘*')
et très performants.
Selon cette
hypothèse,
l'AG recherche le MG
en juxtaposant les briques
qu'il a
identifiées et
mémorisées au
cours du run.
L'accès
à une information
statistique sur la forme du
coût, et la
mémorisation
partielle de cette
information par les
mécanismes
génétiques
expliquent la
réduction du temps
de calcul entre le RS et
l'AG (Figure
14).
Ensuite, le codage des paramètres à partir de leurs valeurs extrêmes admissibles permet une gestion très aisée des domaines de recherche bornés. A l'intérieur de ce domaine, il est possible de modifier ponctuellement le coût pour que l'AG ne soit pas perturbé par les instabilités numériques du modèle (section 6.2.1(c)).
Les expériences décrites dans la section précédente montre que l'AG converge très rapidement vers le proche voisinage du MG, mais qu'ensuite sa progression est très lente. Nous verrons dans la Partie III que cette lenteur n'est pas un inconvénient majeur. En effet, lorsque nous utiliserons des données réelles entâchées d'erreurs nous devrons nous contenter du repérage des bassins d'attraction de certains minima locaux (section 7.1.2).
Comme pour tous les algorithmes de minimisation stochastiques, la convergence de l'AG ne peut pas être garantie. Les procédures de codage des paramètres, de sélection des parents, de crossover et de mutation exigent l'ajustement de plusieurs paramètres. Cependant, il nous a semblé à la lecture de Bäck et Schwefel (1993), de Goldberg (1994), de Carroll (1996 ) et de Schoenauer et Michalewicz (1997) que des règles empiriques mais robustes existent pour fixer leur valeur. Elles font d'ailleurs l'objet de recherches intenses à l'heure actuelle. Le succès de l'AG lors de l'estimation des huit paramètres du modèle est un argument en faveur de la robustesse du code de Carroll (1996 ; Figure 39b-c).
Néammoins, l'application de cette version de l'AG à l'estimation de plusieurs dizaines de paramètres, par exemple pour inverser un modèle d'écosystème planctonique, peut être limitée par le nombre élevé d'intégrations du modèle exigé. Une solution partielle consiste en l'évaluation en parallèle des individus d'une population (modèle maître-esclave, Schoenauer et Michalewicz, 1997). De plus, l'AG n'est qu'une branche des algorithmes évolutifs (Bäck, 1996). Un autre type d'algorithmes évolutifs, encore inappliqué en océanographie, est celui des stratégies évolutives. Il s'agit d'AG"intelligents" dont certains paramètres algorithmiques tels que le taux de mutation évoluent au cours de l'optimisation pour s'adapter à la structure du problème. Ils ont été conçus spécifiquement pour résoudre des problèmes d'estimation paramétrique fortement non-linéaires. Bäck et Schwefel (1993) comparent les différents algorithmes évolutifs sur l'optimisation de trois fonctions théoriques : la convergence des stratégies évolutives est toujours beaucoup plus rapide que celle des AG.
En nous basant sur une série d'inversions simulées, nous avons montré que les AOG sont mieux adaptés à la résolution de problèmes inverses fortement non-linéaires que les algorithmes de minimisation associés à la théorie inverse linéaire (Chapitre 5). En effet, ils sont conçus pour minimiser des fonctions complexes possédant plusieurs minima locaux. Il est important de souligner que leur convergence est empirique et donc non garantie.
Les trois AOG que nous avons testé (TRUST, RS, AG) sont capables de retrouver deux des huit paramètres de PSyDyn utilisés pour fabriquer un jeu de données artificielles non bruitées, dont la structure reflète celle du jeu de données EUMELI. Ils se contentent d'une information a priori sur les inconnues sous la forme de leurs intervalles de valeurs possibles, et n'exigent pas de linéariser localement le problème inverse.
Ces tests montrent que d'une façon générale les algorithmes déterministes tels que le TRUST sont moins bien adaptés à l'estimation des paramètres biogéochimiques que les algorithmes stochastiques dont font partie le RS et l'AG. De plus, la complexité du TRUST rend son application à l'estimation de nombreux paramètres très laborieuse. Le RS s'avère être un algorithme très coûteux en temps de calcul et peu robuste. Enfin, l'AG est facile à appliquer, il est le plus robuste des trois AOG et il converge rapidement vers le bassin d'attraction du MG. Il est le seul capable de retrouver l'ensemble des huit paramètres optimaux. De nombreuses équipes de recherche nationales (dont l'Equipe Evolution Artificielle et Apprentissage de l'Ecole Polytechnique (EEAAX) de M. Schoenaurer, http://www.eeaax.polytechnique.fr/eeaax.html) travaillent au développement des algorithmes évolutifs d'une façon générale. Cela nous assure d'un éventuel soutient informatique pour les applications futures de notre approche.
La Partie III est consacrée à l'application de l'AG à l'assimilation d'un premier jeu de données EUMELI. Elle a pour but la poursuite du développement de notre approche inverse par la prise en compte des incertitudes des mesures in situ et des erreurs du modèle.