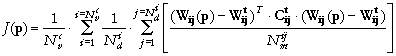Back | Next


Partie III
Inversion à partir de mesures in situ :
exemple de'aluminium au site EUMELI oligotrophe



Chapitre 7 Critère de sélection des paramètres

Dans cette partie, nous nous proposons d'appliquer l'algorithme génétique sélectionné dans le Chapitre 6 à l'assimilation d'un premier jeu de données in situ. Notre objectif est d'estimer les paramètres contrôlant les flux d'Al au site EUMELI oligotrophe. Les propriétés et l'intérêt biogéochimiques de cet élément sont présentées dans la section 10.2.1. Il est principalement utilisé comme traceur de la fraction lithogénique du flux de masse (Maring et Duce, 1987 ; Bory et Newton, 2000 ) : c'est une des fractions dominantes dans cette région (section 2.3.3 ; Tableaux 9 et 10). Ce travail fait l'objet d'un article (Athias et al., 2001) qui est reproduit dans l'Annexe 6.

Le but de ce chapitre est tout d'abord de redéfinir le critère de sélection des vecteurs de paramètres de façon à prendre en compte d'une façon générale la structure des jeux de données réelles ainsi que l'incertitude des mesures in situ. Ensuite, nous décrirons les données in situ et les informations a priori sur les paramètres que nous avons rassemblées pour résoudre notre problème inverse.

7.1 Formulation du critère de sélection

7.1.1 Expression générale de la fonction coût

Dans la section 4.2, nous avons choisi de sélectionner les paramètres du modèle de la colonne d'eau en fonction de leur coût, c'est-à-dire de l'écart entre les observations et les simulations qu'ils génèrent. L' Eq. (10) est une première expression de la fonction coût. Elle est adaptée au contexte des inversions simulées où l'on assimile des pseudo-données non bruitées régulièrement réparties dans le temps et sur la profondeur (section 4.2.2(b)). L'expression suivante est une généralisation de l'Eq. (10). Elle est applicable à des jeux de données réelles de structures variées et prend en compte l'incertitude sur les mesures :

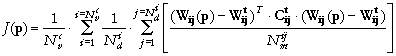. (23)

La constante Nvc désigne le nombre de variables d'état du modèle pour lesquelles on dispose d'observations (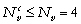, cf. section 3.1.2). Pour la ième variable d'état contrainte (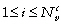), les observations sont disponibles à Ndi profondeurs, et Nmij désigne le nombre de mesures faites à la profondeur j (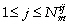). Les observations sont ordonnées dans le () vecteur Wijt. Les simulations sont échantillonnées aux dates et profondeurs d'échantillonnage réelles et rangées dans le () vecteur Wij(p). La (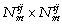) matrice Cijt est l'inverse de la matrice de covariance des erreurs sur les mesures de la ième variable d'état à la profondeur j. Nous supposons que ces erreurs sont distribuées de façon gaussienne et décorrélées dans le temps, dans l'espace et entre les variables d'état : Cijt est une matrice diagonale. Cette approximation est relativement grossière : par exemple, de forts courants latéraux peuvent biaiser la collecte des flux de matière par les pièges sur plusieurs périodes de collecte (section 2.2.2(a)). Nous nous en contenterons cependant, car nous manquons d'information pour calculer les termes de corrélation temporelle. Rappelons que malgré la diversité des variables d'état, J est adimenionnelle.

7.1.2 Prise en compte des incertitudes des données in situ

(a) Définition du domaine des solutions acceptables

Les données réelles que nous cherchons à ajuster sont toutes entachées d'une incertitude généralement élevée:

Dans ce manuscrit, nous considérons que toute donnée peut prendre toutes les valeurs comprises dans l'intervalle de sa barre d'erreur. Sur la base de cette hypothèse, tous les vecteurs de paramètres dont les simulations passent par les barres d'erreur des observations expliquent correctement les mesures, et ils sont équivalents relativement à ces erreurs. Ils sont donc tous des solutions au problème inverse : nous les qualifions de vecteurs de paramètres acceptables (Figure 41).

Etant donnée la normalisation de la fonction coût par rapport au nombre total de données assimilées et aux incertitudes sur les observations (Eq. 23), les vecteurs de paramètres acceptables se caractérisent par un coût inférieur ou égal à 1. Leur ensemble est donc inclus dans l'ensemble des vecteurs de paramètres vérifiant l'inégalité 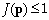, ou domaine acceptable. Dans le cas spécifique des problèmes inverses fortement non-linéaires, à cause de la complexité des fonctions coût qui leur sont associées (section 4.2.2(b)), ce domaine peut être formé de plusieurs bassins disjoints (Figure 42), chacun d'eux pouvant ne pas être convexes (Mazzega, 2000).

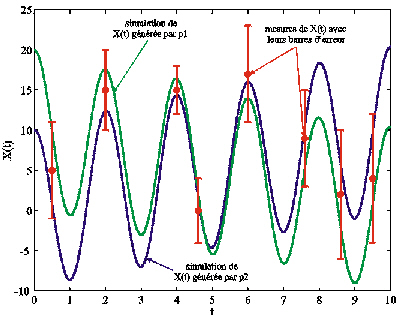
Figure 41. Illustration du critère de sélection des vecteurs de paramètres: tous ceux (tels que p1 et p2) dont les simulations de la variable d'état X(t) passent par les barres d'erreur des mesures les expliquent correctement. Ils sont dits acceptables.

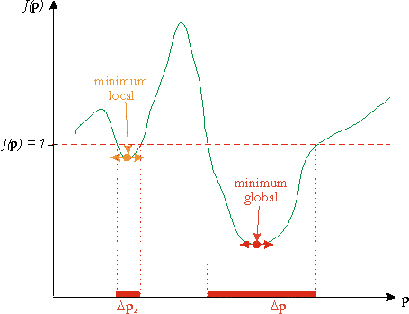
Figure 42. Structure du domaine acceptable: il peut être formé de plusieurs bassins disjoints dont le contour peut être convexe ou concave (Mazzega, 2000). Les vecteurs appartenant aux bassins Dp1 et Dp2sont des solutions inverseséquivalentes vis-à-vis des erreurs sur les données.

La Figure 42 montre qu'à partir du moment où l'on contraint le modèle par des données réelles dont les incertitudes sont significatives, la nature mathématique du problème inverse n'est plus celle que nous avons décrite dans la section 4.2.1 : l'estimation du seul MG de la fonction coût ne résout plus complètement le problème. Résoudre le problème inverse exige maintenant de localiser tous les bassins de vecteurs acceptables à l'intérieur de l'espace de recherche des paramètres de dimension Np = 8. Dans les deux chapitres suivants, nous proposons des stratégies de résolution basées sur l'AG sélectionné dans le Chapitre 6.

(b) Déformations de la fonction coût induites par les erreurs sur les données

Dans la section 4.2.3, nous avons décrit comment la structure du jeu de données assimilé contrôle la forme de la fonction coût, et par conséquent la possibilité d'estimer les paramètres caractéristiques du fonctionnement du système réel. Les erreurs sur les données entraînent elles aussi des modifications des valeurs et de la forme du coût. Supposons que l'on dispose d'un modèle qui soit capable de reproduire exactement la dynamique du système réel. A cause des erreurs de mesure, aucune simulation ne peut être exactement ajustée à toutes les données : la valeur minimale du coût est supérieure à 0. Plus généralement, la présence d'erreurs non corrélées avec le signal des données augmente la moyenne de la fonction coût.

D'autre part, on montre que dans le cas de l'assimilation d'un faible nombre de données (relativement aux échelles temporelles caractéristiques du système réel, cf. section 4.2.3), les erreurs des données peuvent induire une modification de la distribution et de l'ordre relatif des minima locaux du coût (Mazzega, 2000). Cette situation sera illustrée dans la section 8.1.2(a).

7.2 Description des données in situ disponibles

Nous avons constitué une base de données décrivant les flux d'Al dans la colonne d'eau au site O pendant les campagnes EUMELI. Dans le but d'optimiser la détection des paramètres et de limiter la possibilité de dégénérescence du coût, nous avons rassemblé des mesures des quatre variables d'état du modèle COLDO.

7.2.1 Données collectées au site oligotrophe

Les mesures d'Al réalisées au site O ne concernent que les phases des particules piégées et filtrées.

(a) Enregistrement des pièges à particules

La stratégie d'échantillonnage des particules piégées a été décrite dans la section 2.3.2(a). Rappelons que sur les cinq pièges immergés, seuls les échantillons collectés à 1000, 2500 et 4400 m sont exploitables. Le flux de masse a été mesuré aux trois profondeurs. Le flux d'Al n’a été mesuré qu'à partir des échantillons collectés à 1000 et 2500 m. Le principe des mesures analytiques est détaillé par Bory (1997), Bory et Newton (2000) et Bory et al. (2001). Ces données sont représentées sur la Figure 43 ; elles ont été décrites dans la section 2.3.3(a).

Les profils du flux de masse (Fm) et du flux d'Al (Fe) permettant d'initialiser les simulations ont été calculés à partir des mesures faites pendant la période allant du 23 février au 5 mars 1991, selon la procédure décrite dans la section 3.1.3. Les conditions aux limites journalières forçant ces deux variables d'état à 1000 m ont été calculées en utilisant toutes les mesures disponibles entre le 23 février 1991 et le 1er décembre 1992 (Tableau 4 ; section 3.1.3). Les flux mesurés à 2500 et 4400 m sont assimilés : ils définissent les matrices Wijt décrites ci-dessus (Eq. 23).

Le calcul des matrices Cijt exige d'évaluer les erreurs de collecte des pièges et les erreurs des mesures analytiques. Les mesures des traceurs radio-isotopiques réalisées à EUMELI ne permettent pas de quantifier l'efficacité des pièges (section 2.2.2(a)). Nous avons donc appliqué les résultats de Bacon (1996) selon lesquels les pièges situés à 2500 et 4400 m auraient une précision égale à ± 25 % de la moyenne annuelle du flux de masse. Cela correspond à une erreur de collecte du flux de masse de 9,2 et 7,4 mg/m2/j à 2500 et 4400 m respectivement. Les erreurs analytiques ont été estimées par A. Bory (communication personnelle, 2000) pour les échantillons prélevés à 2500 m et pour les deux premiers déploiements uniquement (section 2.3.2(a)). Nous avons calculé que 75 % des erreurs analytiques sur le flux de masse sont inférieures à 3,3 mg/m²/j et que 75 % des erreurs analytiques sur la concentration d'Al sont inférieures à 0,17 %. Nous avons utilisé ces deux valeurs comme erreur analytique a priori pour le troisième déploiement, et pour les mesures du flux de masse à 4400 m.

(b) Mesures des pompes in situ

La stratégie d'échantillonnage des particules filtrées a été décrite dans la section 2.3.2(b). Au site O, les échantillons n'ont été prélevés qu'entre 10 et 1000 m de profondeur (Tableau 6, Figure 43). Le principe de la mesure analytique de la concentration en Al particulaire est détaillé par Tachikawa (1997) et Tachikawa et al. (1999). La base de données EUMELI ne fournit donc qu'une seule donnée à 1000 m pour contraindre la concentration en Al particulaire (Cpe) dans le temps et entre 1000 et 4500 m. Afin de mieux contraindre cette variable d'état, nous avons qualitativement analysé le profil d'Al particulaire mesuré au site M (Tachikawa et al., 1999), ainsi que ceux mesurés pendant la campagne Harmattan (Copin-Montégut et Copin-Montégut, 1983 ; Figure 43). Au cours de cette campagne, douze profils ont été réalisés en mai 1971 entre 10 et 6400 m le long de la côte africaine entre 12°N et l'équateur (Figure 44 ; C. Copin, communication personnelle, 2000). D'une façon générale, la concentration en Al particulaire est constante avec la profondeur, ou diminue légèrement entre 100 m et le fond (Figure 43). Par conséquent, nous avons reconstitué un profil a priori pour le site O en extrapolant le profil existant entre 1000 et 4500 m, à partir de son gradient entre 100 et 1000 m (Figure 43).

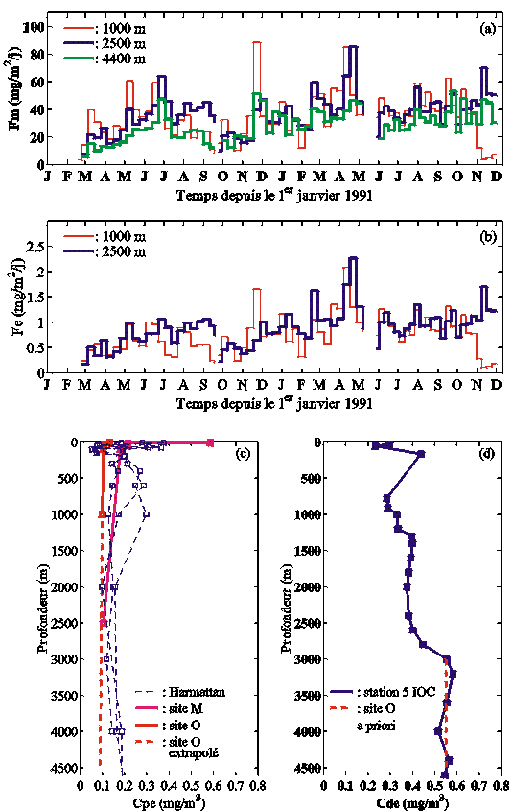
Figure 43. Données in situ utilisées pour estimer les paramètres contrôlant le transfert de l'Al dans la colonne d'eau au site O. Les flux de masse (a) et d'Al (b) ont été mesurés au site O (Bory et Newton, 2000). Le profil d'Al particulaire mesuré au site O (c; Tachikawaet al., 1999) a été extrapolé après l'analyse des profils réalisés au site M et aux stations Harmattan les plus éloignées de la côte africaine (stations 8, 10 et 15 de la Figure 44; Copin-Montégut et Copin-Montégut, 1983). Le profil d'Al dissous (d) a été mesuré à la station IOC n°5 (Measures, 1995).

Ce profil est d'abord utilisé pour initialiser les simulations. Nous ne disposons d'aucune information sur la variabilité temporelle de l'Al particulaire dans cette région, mais Sarthou et Jeandel (2001) montrent que l'Al particulaire a une très faible variabilité temporelle dans la couche profonde en Méditerranée, même si de fortes variations sont observées dans les eaux de surface. Nous avons donc utilisé le profil extrapolé pour contraindre Cpe à chaque pas de temps et de profondeur entre 1100 et 4500 m. Enfin, la valeur mesurée au site O à 1000 m (Cpe = 0,09963 mg/m3) sert de condition aux limites à chaque pas de temps.

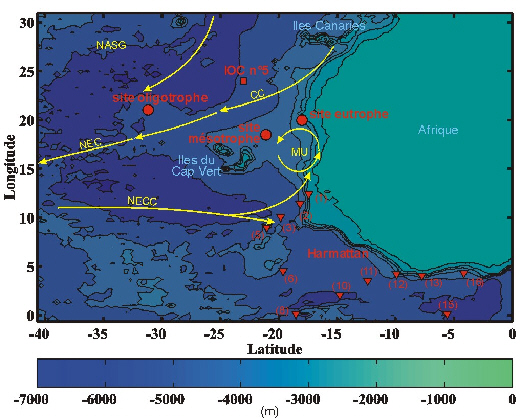
Figure 44. Localisation des stations à partir desquelles la base de données contraignant les flux d'Al au site O a été constituée. Les ronds et les triangles rouges représentent respectivement les stations EUMELI et Harmattan, dont les numéros de stations sont indiqués (Copin-Montégut et Copin-Montégut, 1983). Le carré rouge localise la station IOC n°5. CC: Courant des Canaries; NASG: Gyre Subtropicale Nord Atlantique; NECC: Contre-Courant Nord Equatorial; NEC: Courant Nord Equatorial; MU: Upwelling Mauritanien.

L'incertitude de collecte des pompes in situ porte surtout sur l'évaluation du volume filtré. On estime généralement qu'il est connu avec une précision de 5 % (section 2.2.2(b)). Selon Tachikawa et al. (1999), l'incertitude sur les mesures analytiques est aussi de l'ordre de 5 %.

7.2.2 Données complémentaires

La base de données EUMELI ne contient pas de mesure de la concentration en Al dissous. Pour la compléter, nous avons eu recours à celle constituée dans le cadre de l'"International Oceanographic Commission" (IOC). Son but était de mesurer la concentration d'un grand nombre d'éléments en trace dans les principales masses d'eau profondes. Ces valeurs doivent servir de référence pour quantifier les flux de ces éléments traces liés aux activités anthropiques. Dans ce cadre, quatre profils de la concentration en Al dissous ont été réalisés le long de la côte africaine, entre les mois de mars et d'avril 1990 (Measures, 1995). En particulier la station n°5 (24°N, 23°W) est située à proximité de la région EUMELI (Figure 44).

Cependant, la comparaison des distributions des masses d'eau à la station IOC et à EUMELI montre des différences significatives. Or ces masses d'eau sont caractérisées par des concentrations en Al contrastées (Measures, 1995). Ainsi, les eaux intermédiaires de la station IOC comprises approximativement entre 500 et 1000 m sont composées d'eau méditerranéenne (MOW) et elles ne possèdent aucune des caractéristiques de l'eau antarctique intermédiaire (SAIW ; Measures et al., 1995). A l'opposé, la SAIW est présente aux trois stations EUMELI, et elles ne sont pas atteintes par la MOW (Figure 9 ; Pierre et al., 1994). Ces différences influencent les propriétés des masses d'eau et en particulier leur concentration en Al jusqu'à 2000 m : c'est la partie supérieure de l'eau profonde nord-atlantique (NADW). Cette dernière est relativement hétérogène, et elle n'a pas été suffisamment échantillonnée lors des campagnes EUMELI pour permettre une comparaison rigoureuse avec la station IOC. Par contre, toute la région du plateau du Cap Vert et de la partie sud du Bassin des Canaries est occupée entre 3000 m et le fond par l'eau de fond antarctique (AABW). Elle est caractérisée par une grande homogénéité spatiale (McCartney et al., 1991 ; section 2.3.1).

Comme le profil IOC est le seul que nous ayons à notre disposition, nous avons utilisé sa valeur à 1000 m (0,329 mg/m3) pour forcer Cde à chaque pas de temps (Figure 43). La comparaison des masses d'eau suggère que cette valeur surestime la concentration en Al dissous à 1000 m au site O. Nous reviendrons sur ce point dans la section 8.3.3. Nous ne connaissons pas la variabilité temporelle de l'Al dissous à cette profondeur, mais Pierre et al. (1994) rapportent que la couche comprise entre 800 et 1400 m a une faible variabilité temporelle. Le profil de l'IOC sert également à initialiser les simulations. Cde est contrainte à tous les pas de temps et de profondeur entre 3000 et 4500 m par un profil dont la valeur est la moyenne du profil de l'IOC sur cette couche (0,553 mg/m3 ; Figure 43). Nous avons estimé que les masses d'eau situées au-dessus de 3000 m à la station IOC et aux stations EUMELI sont trop différentes pour que l'on puisse assimiler la partie supérieure du profil.

Selon Measures (1995), les erreurs des mesures analytiques sont de 5,4 %. Les échantillons ont été prélevés avec des bouteilles Go-Flo : on estime généralement que leur volume est connu avec une précision de 5 %.

7.3 Mise en œuvre de l'assimilation

7.3.1 Intégration du modèle

A la différence des expériences d'inversions simulées présentées dans la Partie II, les expériences d'assimilation des données in situ ont toutes été réalisées avec la version COLDO du modèle (section 3.1). Celle-ci est intégrée pour chaque évaluation du coût par l'AG. L’intégration débute par un "spin-up" de un an à partir du 23 février 1991, dont le but est de limiter l'influence des erreurs sur les conditions initiales. Ensuite, le modèle est intégré sur la durée de la campagne EUMELI, soit du 23 février 1991 au 1er décembre 1992. Les mesures in situ sont assimilées à partir de la fin du spin-up.

7.3.2 Configuration de l'algorithme génétique

Pour réaliser les expériences inverses présentées dans le Chapitre 8, nous avons repris exactement le même algorithme que celui que nous avons sélectionné dans le Chapitre 6 (Carroll, 1996). En particulier, les paramètres algorithmiques sont inchangés (section 6.1.3). La fonction coût est minimisée par étapes de 50 générations. Nous avons empiriquement choisi d'arrêter l'exploration du coût au moment où un meilleur individu a survécu pendant plus de 50 générations.

7.3.3 Délimitation de l'espace de recherche

Comme nous l'avons démontré dans la section 4.2.2(b), la complexité des fonctions coût associées à l'estimation des paramètres de COLDO exige de tous les optimiser simultanément (Figure 27). Nous avons réalisé quelques expériences inverses préliminaires en utilisant les intervalles de recherche décrits dans le Tableau 16 et calculés à partir d'une compilation bibliographique. En particulier, la valeur maximale de la vitesse de chute des particules piégées (Vgmax = 200 m/j) est basée sur l'évaluation proposée par Bory et Newton (2000) selon laquelle au site O Vg ~150 m/j. Nous avons constaté que l'AG avait tendance à "se cogner" sur la limite supérieure de Kad et Vg. Nous avons arbitrairement augmenté la valeur maximale de Kad de telle façon que Krpmax = Kadmax = 0,356 /j, et nous avons fixé Vgmax à 800 m/j pour couvrir toute la gamme des valeurs possibles de ce paramètre (Whitfield et Turner, 1987). Les limites de l'espace de recherche des paramètres, qui correspondent à l'information a priori sur les inconnues, sont reportées dans le Tableau 18.

7.4 Conclusion du chapitre

Nous avons construit une base de données permettant de contraindre au mieux dans le temps et dans l'espace toutes les variables d'état du modèle COLDO décrivant le transfert de l'Al dans la colonne d'eau au site O. Nous avons également délimité l'espace de recherche des paramètres contrôlant ce transfert, à partir de valeurs relevées dans la littérature.

Nous avons choisi de considérer comme acceptable tout vecteur de paramètres générant des simulations passant par les barres d'erreur des données assimilées, c'est-à-dire dont le coût est inférieur ou égal à 1.


Chapitre 8 Expériences d'inversion

A partir de la base de données in situ présentée dans le Chapitre 7, nous avons réalisé six expériences d'inversion, dont les objectifs sont rappelés dans le Tableau 17. Il s'agit :

Les résultats des six expériences sont synthétisés dans le Chapitre 9.

8.1 Identification de la structure du jeu de données à assimiler

8.1.1 Expérience A : assimilation des mesures des pièges à particules

Pour cette première expérience, nous n'avons assimilé que les mesures in situ échantillonnées pendant la campagne EUMELI au site O, c'est-à-dire celles des pièges à particules (Figure 43a-b). Les profils d'Al particulaire et dissous que nous avons calculés (sections 7.2.1(b) et 7.2.2) sont utilisés pour évaluer a posteriori les simulations générées par les solutions détectées par l'AG.

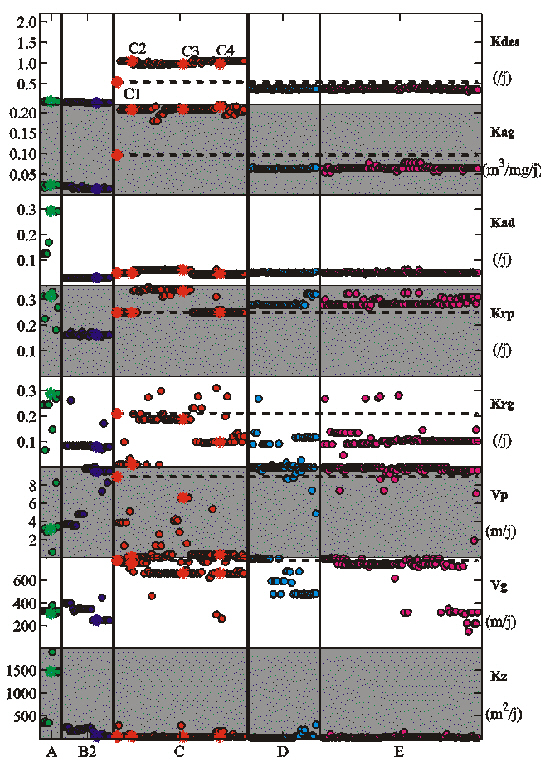
Figure 45. Représentation des solutions acceptables trouvées lors des exps. A, B2, C, D et E (Tableau 17). Au cours de chaque expérience (délimitée par les traits épais verticaux noirs), dès que l'AG détecte un nouveau vecteur de paramètres acceptables, ses 8 composantes sont reportées par un rond coloré sur une verticale, immédiatement à droite du vecteur précédent. Pour chaque paramètre, l'axe des ordonnées correspond à l'intervalle de ses valeurs possibles (Tableau 18). Les simulations générées par les solutions indiquées par 8 étoiles dans les panneaux des exps. A et B2 sont représentées sur les figures 46 et 50 respectivement. Pour l'exp. C, les 4 solutions désignées par des étoiles sont, de gauche à droite, les solutions C1, C2, C3 et C4 (Tableaux 18 et 20). La solution C1 génère les simulations représentées sur la Figure 52. Les 8 lignes tiretées noires servent à comparer la solution C1 à celles trouvées au cours des exps. D et E (Tableau 17).

Expérience

A

B1

Données assimilées

mesures des pièges à particules au site EUMELI O (Figure 43a-b)

toutes les pseudo-données générées avec COLDO (Figure 47)

Données perturbées

aucune

aucune

Modèle intégré

COLDO original (Eqs. 2 à 5)

COLDO original (Eqs. 2 à 5)

Objectifs

définir la structure du jeu de données à assimiler pour contraindre les paramètres contrôlant les flux d'Al au site EUMELI O

§ définir la structure du jeu de données à assimiler pour contraindre les paramètres contrôlant les flux d'Al au site EUMELI O

§établir des règles d'interprétation des résultats des inversions réelles

Représentation des solutions

Figures 45 et 51

Figure 48

Représentation de simulations générées par les solutions

Figure 46

Figure 47

Tableau 17. Caractéristiques des expériences d'inversion présentées dans le Chapitre 8.

Expérience

B2

C

Données assimilées

toutes les données in situ (Figure 43)

toutes les données in situ (Figure 43)

Données perturbées

aucune

aucune

Modèle intégré

COLDO original (Eqs. 2 à 5)

COLDO avec la nouvelle équation du flux de masse (Eqs. 3 à 5 et 25)

Objectifs

§ générer des estimations des paramètres contrôlant les flux d'Al au site EUMELI O

§étudier la robustesse des solutions de l'exp. C vis-à-vis de la paramétrisation de l'agrégation

générer des estimations des paramètres contrôlant les flux d'Al au site EUMELI O

Représentation des solutions

Figures 45 et 51

Figures 45 et 51

Représentation de simulations générées par les solutions

Figure 50

Figures 52 à 58

Tableau 17 (suite)

Expérience

D

E

Données assimilées

toutes les données in situ (Figure 43)

toutes les données in situ (Figure 43)

Données perturbées

données in situ assimilées

données in situ utilisées comme conditions aux limites

Modèle intégré

COLDO avec la nouvelle équation du flux de masse (Eqs. 3 à 5 et 25)

COLDO avec la nouvelle équation du flux de masse (Eqs. 3 à 5 et 25)

Objectifs

étudier la robustesse des solutions de l'exp. C vis-à-vis des erreurs des don-nées in situ assimilées

étudier la robustesse des solutions de l'exp. C vis-à-vis des erreurs des don-nées in situ utilisées comme conditions aux limites

Représentation des solutions

Figures 45 et 51

Figures 45 et 51

Représentation de simulations générées par les solutions

-

-

Tableau 17 (suite)

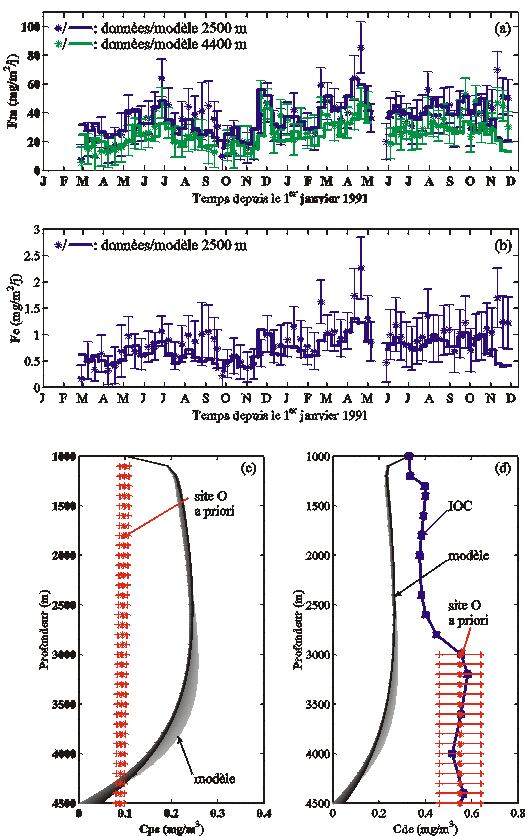
Figure 46. Flux de masse (a), d'Al (b), Al particulaire (c) et dissous (d) simulés par le vecteur de paramètres acceptables trouvé lors de l'exp. A (Tableau 17) et indiqué par 8 étoiles vertes sur la Figure 45. Les simulations sont comparées aux mesures des pièges à particules (a-b) qui ont été assimilées et aux profils calculés des phases filtrée et dissoute, qui n'ont pas été assimilés. Les profils simulés de Cpe et Cde sont d'autant plus récents qu'ils sont sombres.

Le critère d'arrêt de la minimisation par l'AG (section 7.3.2) a été atteint après que 350 générations aient été estimées (soit 1750 calculs du coût). Il a détecté 9 vecteurs de paramètres acceptables, dont le coût varie entre 0,99 et 0,79 : ils sont représentés sur la Figure 45. Les valeurs de Kdes, Kag et Vg semblent contraintes de façon unique par les données, mais celles des autres paramètres sont très dispersées. En particulier, Kad et Kz semblent pouvoir prendre des valeurs appartenant à deux intervalles distincts. Cela suggère que le domaine acceptable est constitué d'au moins deux bassins disjoints. La Figure 46 représente les simulations générées par l'une des solutions. En accord avec le critère de sélection formulé par la fonction coût (Eq. 23), les simulations sont cohérentes avec les mesures des pièges étant données leurs incertitudes. Le modèle a tout de même tendance à surestimer la décroissance du flux de masse entre 2500 et 4400 m, ainsi que le temps de transfert des évènements de flux élevés entre ces profondeurs (Figure 43a-b). Par contre, les valeurs et la forme des profils simulés d'Al particulaire et dissous sont irréalistes. Cette caractéristique est valable pour les simulations calculées à partir des 9 vecteurs acceptables.

Cette expérience montre que l'ajustement du modèle aux seules mesures des pièges à particules n'est pas un critère suffisant pour sélectionner les paramètres expliquant la distribution de l'Al au site O.

8.1.2 Assimilation de toutes les données disponibles

(a) Expérience B1 : une inversion simulée préliminaire

Avant d'assimiler toutes les données de la base que nous avons constituée (section 7.2), nous avons réalisé une expérience inverse simulée, de façon à définir des règles d'interprétation des résultats des expériences réelles.

Symbole

Intervalle de recherche

Valeur optimale

Solution C1


Limite inférieure

Limite supérieure

Source

(exp. B1)

(exp. C)

Paramètres biogéochimiques

Kdes (/j)

0,0000

2,2000

1

0,0415

0,5404

Kag (m3/mg/j)

0,0000

0,2200

1

0,0141

0,0971

Kad (/j)

0,0000

0,3560

1

0,0316

0,0503

Krp (/j)

0,0000

0,3560

1

0,1627

0,2508

Krg (/j)

0,0000

0,3560

1

0,0792

0,2098

Paramètres physiques

Vp (m/j)

0,00

10,00

2

9,53

8,90

Vg (m/j)

0,00

800,00

2

246,33

776,54

Kz (m2/j)

25,00

2000,00

3

57,80

50,08

Sources : 1. cf. Tableau 14 ; 2. Whitfield et Turner (1987) ; 3. Zakardjian et Prieur (1994) ; L. Prieur, communication personnelle (1997).

Tableau 18. Valeurs des paramètres du modèle COLDO mentionnées dans les expériences d'assimilation des données in situ décrivant le transfert de l'Al au site O (Tableau 17).


Fabrication d'un jeu de pseudo-données

Nous avons généré un jeu de pseudo-données à partir du modèle COLDO, en utilisant le vecteur de paramètres indiqué dans le Tableau 18. Les pseudo-données sont représentées sur la Figure 47. Les conditions initiales et conditions aux limites sont celles qui ont été décrites dans la section 7.2. Le modèle est intégré selon le schéma mentionné dans la section 7.3.1.

Ainsi, la résolution spatio-temporelle du jeu de pseudo-données est exactement identique à celle du jeu de données réelles.

Assimilation des pseudo-données

Dans cette expérience, toutes les pseudo-données ont été assimilées. Le critère d'arrêt de l'exploration du coût par l'AG a été atteint après qu'il ait évalué 250 générations (soit 1250 valeurs du coût). Il a détecté 140 solutions acceptables, dont le coût varie entre 0,99 et 0,30 (Figure 48). La Figure 47 montre qu'en accord avec le critère de sélection (section 7.1), les simulations calculées avec les solutions acceptables sont cohérentes avec les pseudo-données étant donné le bruit qui leur a été ajouté. Ce résultat suggère que l'estimation des paramètres contrôlant le transfert d'Al au site O exige d'assimiler l'ensemble des données in situ disponibles (section 7.2).

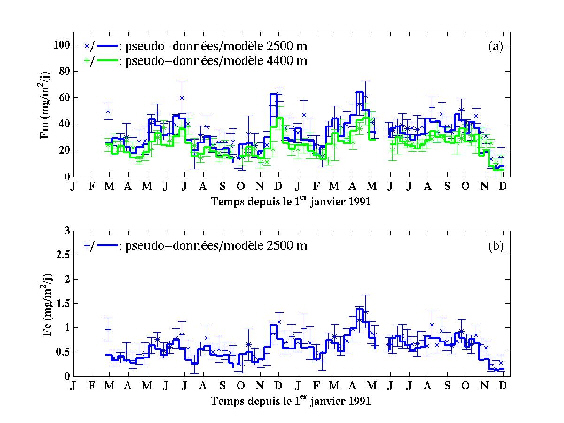
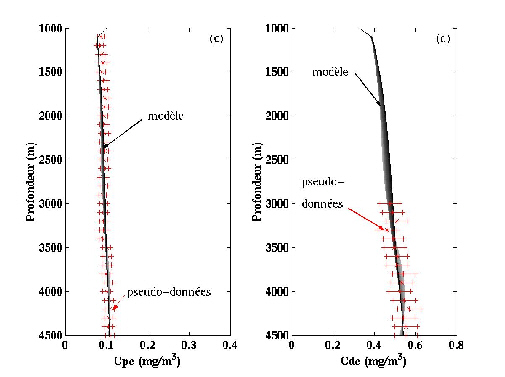
Figure 47. Flux de masse (a), d'Al (b), Al particulaire (c) et dissous (d) simulés par l'un des vecteurs de paramètres acceptables trouvé lors de l'inversion simulée B1 (Tableau 17; Figure 48). Les simulations sont comparées aux pseudo-données calculées par COLDO avec le vecteur de paramètres indiqué dans le Tableau 18. Les profils simulés de Cpe et Cde sont d'autant plus récents qu'ils sont sombres.

Figure 48. Représentation des solutions acceptables au fur et à mesure de leur détection par l'AG lors de l'inversion simulée B1 (Tableau 17). Leurs composantes sont reportées par 8 points rouges sur une verticale dans le cadran correspondant à chaque paramètre, dont les gammes de valeurs possibles sont indiquées sur l'axe des ordonnées. Les 8 étoiles noires désignent le vecteur utilisé pour calculer les simulations de la Figure 47. Les 8 lignes noires tiretées désignent les paramètres utilisés pour calculer le jeu de pseudo-données (Tableau 18).

Cependant, la Figure 48 montre que l'AG n’a pas réussi à retrouver le jeu de paramètres optimal (Tableau 18). Même si les valeurs de certains paramètres (tels que celles de Kdes, Kag, Kad, Krg, Vp et Kz) sont parfois retrouvées, les vecteurs acceptables qui leur sont associés peuvent être éloignés du vecteur optimal dans l'espace de recherche à Np = 8 dimensions. Par exemple, ils peuvent se trouver dans un bassin distinct du bassin d'attraction du MG. Rappelons que lors de l'expérience inverse simulée décrite dans la section 6.2.2, l'AG a été capable de retrouver les 8 paramètres optimaux utilisés pour calculer un jeu de pseudo-données non bruité. Le présent échec peut s'expliquer de trois façons :

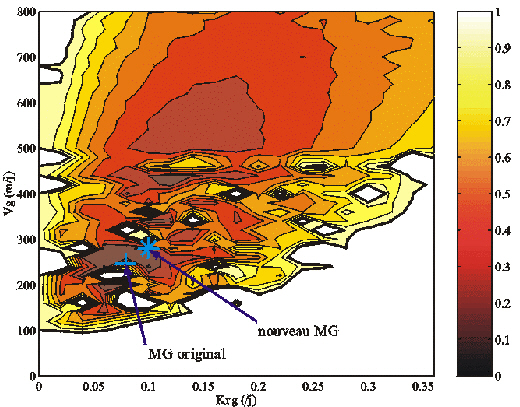
Figure 49. Coupe de la fonction coût associée aux pseudo-données calculées pour l'inversion simulée B1 (Tableau 17) en fonction de Krg et Vg. Les valeurs des autres paramètres sont égales aux valeurs optimales (Tableau 18). La ligne noire épaisse localise l'isocontour J(p) = 1. La croix et l'étoile bleues illustrent la migration du Minimum Global (MG) dûe au bruit ajouté aux pseudo-données.

Cette expérience illustre comment l'existence d'erreurs significatives sur les données assimilées modifie la nature mathématique du problème inverse. La détection du MG ne signifie pas que l'on a identifié les paramètres caractéristiques du fonctionnement du système réel. Comme nous l'avons expliqué dans la section 7.1.2, la solution au problème inverse est incluse dans ce que nous avons appelé le domaine acceptable délimité par l'isocontour J(p) = 1. Il contient tous les vecteurs de paramètres qui expliquent correctement les données in situ disponibles, étant données leurs barres d'erreur. La Figure 49 démontre que la structure du domaine acceptable est très complexe. L'isoligne J(p) = 1 entoure une région très vaste relativement aux intervalles des valeurs possibles de Krg et Vg, à l'intérieur de laquelle se trouvent de petits domaines non-acceptables.

Or, l'AG n'a pas été conçu pour identifier ce type de solutions (section 6.1.3). Il ne permet que de repérer les quelques solutions acceptables évaluées lors de sa progression vers le MG. Pour améliorer la solution, deux stratégies complémentaires sont envisageables. Il s'agit :

Remarque à propos du calcul du calcul systématique de la matrice Hessienne du coût

Après l'inversion d'un modèle, il est fréquent de vérifier si les paramètres associés à "la solution" - en supposant qu'elle est unique - sont contraints de façon indépendante par les données assimilées (Matear, 1995; Vallino, 2000). La méthode utilisée appartient à la théorie inverse linéaire (section 5.1.1). Il s'agit d'évaluer localement le rang de la matrice Hessienne :

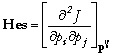(24)

où pg doit se trouver dans le bassin d'attraction du MG. Cela revient à rechercher les directions des dégénérescences éventuelles du coût. L'expérience (exp.) B1 montre qu'à partir du moment où l'on doit prendre en compte les erreurs sur les données in situ, on ne doit plus se préoccuper de la forme du coût autour du MG (le MG n'a d’ailleurs pas plus de valeur que les autres vecteurs de paramètres acceptables), mais de celle du contour J(p) = 1 autour du ou des bassin(s) acceptable(s). Autrement dit, les dégénérescences du coût repérées à l'intérieur du domaine acceptable ne sont pas significatives étant données les erreurs sur les mesures assimilées. En outre, dans le cas non-linéaire, il est peu probable qu'elles reflètent la forme du contour J(p) = 1 , dans la mesure où le domaine acceptable peut englober plusieurs bassins d'attraction (Figure 42). Mais le calcul systématique de l'isocontour J(p) = 1 est un problème mathématique complexe, pour lequel nous ne connaissons pas de méthode.

(b) Expérience B2 : inversion contrainte par toutes les données réelles

Cette expérience correspond à l'assimilation de toutes les données in situ que nous avons rassemblées pour contraindre les flux d'Al au site O (section 7.2, Figure 43).

Le critère d'arrêt de l'exploration par l'AG a été atteint après l'évaluation de 300 générations (i.e. 1500 calculs du coût), et l'AG a détecté les 25 vecteurs de paramètres acceptables représentés sur la Figure 45. Leur coût varie entre 1,00 et 0,81. La Figure 50 représente les simulations calculées à partir de l'une de ces solutions. Le modèle a toujours tendance à surestimer la diminution des flux de masse et d'Al entre 1000 et 2500 m, mais la surestimation de la décroissance du flux de masse entre 2500 et 4400 m est moins prononcée que sur la Figure 46. Le décalage temporel entre les évènements de flux élevés à 1000 et 2500 m est bien reproduit, mais le décalage temporel entre 2500 et 4400 m est trop long. Contrairement à l'exp. A, les profils simulés de Cpe et Cde sont réalistes. Cette expérience confirme qu'il est nécessaire d'ajuster COLDO à des mesures de toutes ses variables d'état pour trouver des paramètres expliquant les flux d'Al au site O.

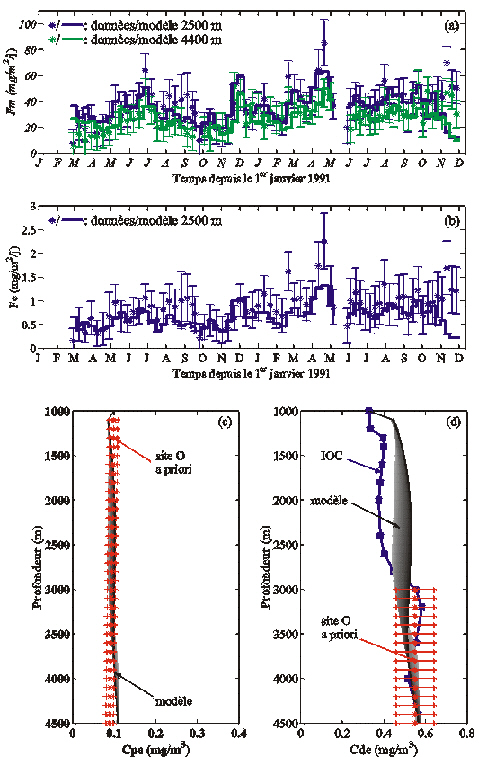
Figure 50. Flux de masse (a), d'Al (b), Al particulaire (c) et dissous (d) simulés par le vecteur de paramètres acceptables trouvé lors de l'exp. B2 (Tableau 17), et indiqué par 8 étoiles bleues sur la Figure 45. Ils sont comparés aux mesures des pièges à particules et aux profils calculés pour les phases filtrée et dissoute qui ont tous été assimilés. Les profils simulés de Cpe et Cde sont d'autant plus récents qu'ils sont sombres.

La Figure 45 montre qu'aucune des solutions de cette expérience ne correspond à celles de l'exp. A. Cela démontre que les estimations des paramètres dépendent des données assimilées, donc des stratégies de mesure en mer. De plus, le domaine acceptable associé à l'assimilation de toute la base de données n'est pas inclus dans le domaine acceptable associé à l'assimilation des seules mesures des pièges. Il est donc nécessaire d'assimiler simultanément - et non successivement - toutes les données dont on dispose. Par rapport à l'exp. A, on constate que les valeurs de Kad, Krp et Kz sont moins dispersées. Cela confirme que l'ajout de mesures fait disparaître certaines dégénérescences de la fonction coût (section 4.2.3). Aucune mesure des paramètres n'existe à laquelle nous pourrions comparer les valeurs trouvées. Bory et Newton (2000) ont estimé la vitesse de chute des grosses particules à Vg ~ 150 m/j à partir du décalage des séries temporelles des pièges à 1000 et 2500 m. Nos valeurs sont beaucoup plus élevées : elles varient entre 244,77 et 446,53 m/j.

Nous avons calculé les rapports Krp/Krg, Krp/Kad et Vg/Vp associés aux solutions acceptables de l'exp. B2. Leurs valeurs sont reportées sur la Figure 51 et dans le Tableau 19. On constate qu'elles sont mieux contraintes que les valeurs de chaque paramètre (Figure 45). Ainsi, Krp/Krg varie entre 1,86 et 2,31, hormis pour deux solutions pour lesquelles les valeurs de Krg sont très élevées. Le rapport Krp/Kad est aussi bien contraint puisqu'il varie entre 5,00 et 5,67. Les valeurs du rapport des vitesses Vg/Vp sont plus dispersées, allant de 24,28 à 107,98. Soulignons que ces intervalles de valeurs sont très probablement discontinus.

8.2 Amélioration de la paramétrisation des processus

8.2.1 Paramétrisation de l'agrégation des petites particules

Par construction, l'exp. B2 fournit certaines des simulations de COLDO les mieux ajustées aux données in situ (Figure 50). Cependant, ces simulations et celles qui ont été calculées à l'issue de l'exp. A (Figure 46) mettent en évidence un défaut systématique de COLDO. En effet, le modèle surestime toujours la décroissance des flux de masse et d'Al avec la profondeur. D'autre part, il prédit un décalage temporel de 10 à 20 jours entre les évènements de flux élevés à 2500 et 4400 m, alors que la plupart de ces évènements se produisent simultanément aux deux profondeurs relativement à la période de collecte des pièges (~10 jours, cf. section 2.3.2(a) ; Figure 43). Or nous avons mentionné que le modèle néglige l'effet de l'agrégation des particules filtrées sur le flux de masse (Eq. 2, section 3.1.2). Les travaux récents de Arraes-Mescoff (2000) suggèrent que cet effet doit être pris en compte.

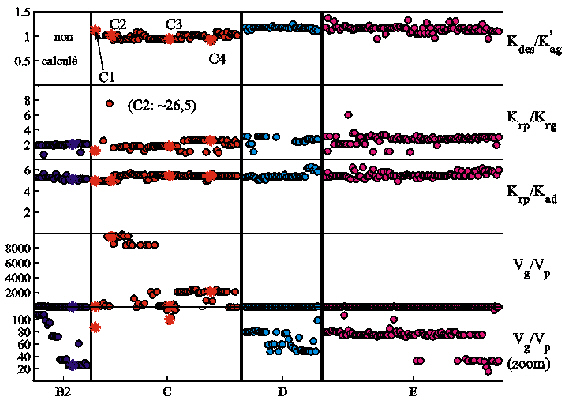
Figure 51. Représentation des rapports Kdes/Kag', Krp/Krg, Krp/Kad et Vg/Vp associés aux solutions acceptables des exps. B2, C, D et E (Tableau 17; Figure 45). Le mode de représentation est le même que pour la Figure 45: pour chaque expérience (délimitée par les traits épais verticaux noirs), à chaque fois que l'AG détecte une nouvelle solution acceptable, les 4 ou 5 rapports qui lui sont associés sont reportés par autant de ronds sur une verticale, dans le cadran qui leur correspond. Le paramètre Kag' n'a pas été défini pour l'exp. B2. Les valeurs extrêmes des rapports associées à chaque expérience sont reportées dans le Tableau 19. La solution de l'exp. B2 désignée par les étoiles bleues génère les simulations de la Figure 50. Les quatre solutions de l'exp. C désignées par des étoiles rouges sont, de gauche à droite, les solutions C1, C2, C3 et C4 (Tableau 20).

Jusqu'à présent, l'effet de l'agrégation des particules filtrées sur le flux de masse n'était pas décrit en partie parce que la concentration totale des particules filtrées (en mg/m3) est difficile à mesurer avec les pompes in situ utilisées pendant les campagnes EUMELI (section 2.2.2(b)). Nous proposons d'estimer cette variable au cours de l'intégration du modèle à partir des simulations de la concentration en Al dans les particules filtrées (Cpe). Pendant la campagne Harmattan déjà mentionnée dans la section 7.2.1(b), des profils de la concentration en Al particulaire filtré et de la concentration totale en particules filtrées ont été réalisés simultanément à partir de bouteilles Niskin (C. Copin, communication personnelle, 2000). A partir de ceux-ci, on en déduit que la proportion moyenne en Al dans ces particules entre 1000 m et le fond, pour les stations les plus éloignées de la côte vaut re = 2,0 % (stations 8, 10 et 15, cf. Figure 44). Nous supposons que cette proportion est représentative du site O, et que sa variabilité verticale et temporelle est négligeable. Ainsi, 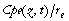est une estimation de la concentration totale en particules filtrées à la profondeur z et à la date t. Nous proposons de remplacer l'équation originale du flux de masse (Eq. 2) par l'équation suivante :

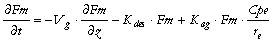(25)

Le terme d'agrégation est le dernier terme de droite. Il est non-linéaire et similaire à celui de l'équation du flux d'Al (Eq. 3). Ce terme induit le couplage de l'équation du flux de masse avec les autres équations du modèle (Eqs. 3-5).

8.2.2 Expérience C : inversion de la version améliorée du modèle COLDO

Cette expérience consiste en l'inversion de la nouvelle version du modèle, basée sur les équations (25) et (3) à (5). A part cette modification des équations, elle est exactement identique à l'exp. B2, c'est-à-dire que toute la base de données est assimilée. L'exploration de la fonction coût s'est arrêtée après l'évaluation de 250 générations (i.e. 1250 calculs du coût). L'AG a détecté 70 vecteurs de paramètres acceptables, dont le coût varie entre 1,00 et 0,79. Ils sont représentés sur la Figure 45.

La Figure 52 représente les simulations calculées par le vecteur de paramètres acceptables indiqué par les étoiles rouges sur la Figure 45, et dont les valeurs sont données dans le Tableau 18. Dans la suite, nous le désignerons par "solution C1" . On constate une amélioration significative de la simulation du transfert du flux de masse entre 2500 et 4400 m. La nouvelle version du modèle reproduit la simultanéité des évènements de flux élevés à ces deux profondeurs, ainsi que la faible diminution du flux de masse entre 2500 et 4400 m qui sont observées pendant les deux derniers déploiements des pièges (Figure 43).

Cependant, le modèle sous-estime la diminution plus importante du flux de masse entre 2500 et 4400 m observée pendant le premier déploiement. Il a également tendance à sous-estimer le temps de transfert des flux de masse et d'Al entre 1000 et 2500 m. Leur diminution entre 1000 et 2500 m pendant les évènements où les flux sont élevés est quant à elle surestimée. Par définition, le modèle est incapable de reproduire la variabilité temporelle et verticale des processus, dans la mesure où les paramètres contrôlant ces processus sont supposés indépendants de la profondeur et du temps (section 3.1.2). Enfin, le modèle sous-estime les flux de masse et d'Al à 2500 et 4400 m de juillet à septembre 1991, et de novembre à décembre 1992. Cela s'explique par le sous-échantillonnage du piège fixé à 1000 m (section 2.3.3(a)) : il induit une erreur dans les conditions aux limites de Fm et Fe. Nous reviendrons sur l'influence des erreurs des conditions aux limites dans la section 8.3.3.

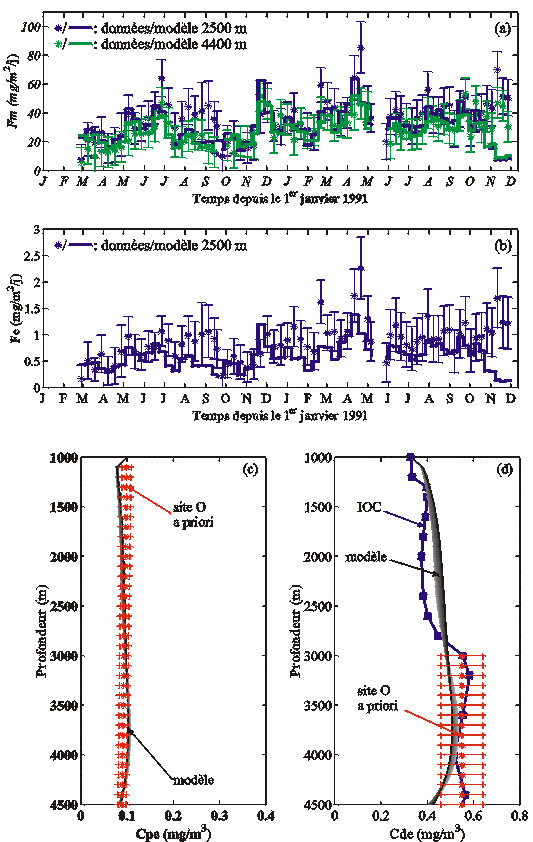
Figure 52. Flux de masse (a), d'Al (b), Al particulaire (c) et dissous (d) simulés par la solution acceptable C1 trouvée lors de l'exp. C (Tableau 17), et indiquée par 8 étoiles rouges sur la Figure 45. Les simulations sont comparées aux mesures des pièges à particules et aux profils calculés pour les phases filtrée et dissoute qui ont tous été assimilés. Les profils simulés de Cpe et Cde sont d'autant plus récents qu'ils sont sombres.

La Figure 45 montre que les solutions acceptables de cette expérience sont différentes de celles trouvées pour l'exp. B2. Les valeurs de tous les paramètres, et en particulier celles de Krg, Vp et Vg sont plus dispersées. Cela peut s'expliquer par l'augmentation de la complexité du système d'équations : il est maintenant complètement couplé et comprend trois termes non-linéaires. On constate également que les valeurs de Kdes, Kag, Krp et Vg sont plus élevées que pour l'exp. B2. Les valeurs de Vg sont pratiquement toutes supérieures à 600 m/j, c'est-à-dire plus de trois fois supérieures aux valeurs que l'on trouve classiquement dans la littérature (~100– 200 m/j ; Deuser et al., 1990; Asper et al., 1992; Newton et al., 1994). Deux valeurs plus faibles ont été trouvées (~299 et ~262 m/j ; cf. Figure 45), mais elles ne permettent pas de reproduire la simultanéité des flux (relativement à la période de collecte des pièges) entre 2500 et 4400 m. Certaines de ces solutions ne sont plus acceptables si les simulations sont calculées avec le modèle COLDO original (Eqs. 2 à 5). Par exemple, le coût de la solution C1 dans ces conditions est ~2,5. Ainsi, l'exp. C démontre que la dynamique du modèle et par conséquent les solutions au problème inverse sont très sensibles à la paramétrisation de l'agrégation. On dit que COLDO a une faible stabilité structurale (Wiggins, 1990).

Les solutions de cette expérience ont en commun la valeur de certains des rapports de paramètres introduits dans la section 8.1.2(b). Le rapport des constantes de dissolution (Krp/Krg) peut varier entre 1,00 et 40,00, mais la plupart des valeurs sont comprises entre 1,00 et 2,68 (Figure 51, Tableau 19). Le rapport Krp/Kad varie entre 4,86 et 5,73. Les valeurs de ces deux rapports sont très proches de celles trouvées pour l'exp. B2, ce qui signifie qu'ils sont relativement robustes vis-à-vis de la paramétrisation de l'agrégation. Le rapport des vitesses de chute des particules reste très variable, allant de 87,27 à ~10 000. Etant donnée la nouvelle équation du flux de masse (Eq. 25), nous avons introduit une pseudo-constante d'agrégation dont l'unité est le j-1, soit Kag', dans le but de comparer l'importance relative de l'agrégation et de la désagrégation sur la variabilité du flux de masse :

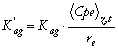. (26)

Dans cette expression, 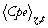est la moyenne au cours du temps et sur la verticale de Cpe(z,t) ; elle vaut 0,0996 mg/m3. Le rapport Kdes/Kag' des solutions acceptables varie entre 0,90 et 1,12 (Figure 51, Tableau 19).

8.3 Ebauche d'une analyse de la robustesse des solutions

L'exp. C a permis de trouver des vecteurs de paramètres dont les simulations expliquent de façon satisfaisante les flux d'Al au site EUMELI O (Figure 52). Les figures 45 et 51 montrent que ces vecteurs sont nombreux, et que certaines de leurs composantes sont mal contraintes par les données in situ. Pour améliorer la résolution du problème, nous proposons de limiter la taille du domaine acceptable en raffinant le critère de sélection des solutions. Etant donnée l'importance de l'incertitude sur la paramétrisation des processus et des erreurs sur les mesures utilisées, nous nous sommes intéressés à la robustesse des solutions vis-à-vis :

Exp. B2

Exp. C

Solution C1

Exp. D

Exp. E

Kdes/Kag'

non défini

0,90 - 1,12

1,12

1,11 - 1,25

0,95 - 1,37

Krp/Krg

1,86 - 2,31

1,00 - 2,68

1,19

1,05 - 3,13

1,01 - 6,05

Krp/Kad

5,00 - 5,67

4,86 - 5,73

4,99

5,08 - 5,36

4,94 - 6,27

Vg/Vp

24,28 - 107,98

87,27 - 9822,33

87,27

48,00 - 98,83

15,81 - 115,45

Tableau 19. Valeurs extrêmes de certains rapports de paramètres de COLDO délimités par les expériences d'inversion présentées dans le Chapitre 8 (Tableau 17). Etant donnée la nature éventuellement discontinue des domaines acceptables, ces intervalles peuvent eux-mêmes être discontinus. Les rapports associés à la solution C1 (Tableau 18) appartiennent aux intervalles délimités par les exps. D et E.

8.3.1 Robustesse des solutions vis-à-vis de la paramétrisation de l'agrégation

La comparaison des résultats des exps. B2 et C (Tableau 17, section 8.2.2) montre qu'aucune des solutions de l'exp. C n'est robuste vis-à-vis de la paramétrisation de l'agrégation (Figure 45). Par contre, les rapports Krp/Krg et Krp/Kad associés à ces solutions sont relativement robustes (Figure 51, Tableau 19). On constate que la solution C1 est la seule solution dont les trois rapports de paramètres - Krp/Krg, Krp/Kad et Vg/Vp - appartiennent aux intervalles de valeurs délimités par l'exp. B2.

8.3.2 Robustesse des solutions vis-à-vis des erreurs sur les données assimilées

(a) Perturbation des données

Pour analyser la robustesse des solutions de l'exp. C vis-à-vis des erreurs des données assimilées, nous avons perturbé chaque donnée de façon aléatoire, et successivement à l'intérieur de sa barre d'erreur de collecte et de sa barre d'erreur analytique (section 7.2). Ensuite, nous avons inversé la nouvelle version de COLDO (Eqs. 25, 3 à 5) en assimilant toute la base des données ainsi perturbées.

(b) Expérience D : inversion à partir des données perturbées

L'AG s’est arrêté après avoir évalué 200 générations (i.e. 1000 valeurs du coût). Il a identifié 36 vecteurs de paramètres acceptables, dont le coût varie entre 1,00 et 0,76. La Figure 45 montre une nette réduction de la dispersion des valeurs des paramètres par rapport à l'exp. C. Il semblerait que l'ajout de bruit aux données assimilées lisse la fonction coût, et fasse disparaître certains bassins acceptables. En particulier, les valeurs de Kdes, Kag et Kad sont pratiquement identiques pour toutes les solutions. Dans une moindre mesure, la dispersion de Vp et Vg est également plus faible.

L'AG n’a retrouvé aucune des solutions de l'exp. C. Néammoins, les valeurs des paramètres apparemment bien contraints, tels que Kdes, Kag, Kad, et Kz sont proches des valeurs de certaines des solutions de l'exp. C. On constate que la solution C1 est très proche - dans l'espace de recherche des paramètres à Np = 8 dimensions - d'un ensemble de solutions de l'exp. D (Figure 45). La valeur de Krg les distingue, mais ce paramètre est particulièrement mal contraint. De plus, la valeur de Krg de la solution C1 appartient à l'intervalle des valeurs délimité par l'exp. D. Ces observations qualitatives suggèrent que la solution C1 se trouve dans un bassin acceptable robuste vis-à-vis des erreurs sur les données assimilées.

Les rapports Kdes/Kag', Krp/Krg et Krp/Kad associés aux solutions de l'exp. D appartiennent aux gammes de valeurs délimitées par l'exp. C (Figure 51 ; Tableau 19). Le rapport Kdes/Kag' varie entre 1,11 et 1,25. Les valeurs du rapport des constantes de dissolution restent assez dispersées puisqu'elles peuvent atteindre des valeurs proches de 600, mais la plupart des valeurs sont comprises entre 1,05 et 3,13. Le rapport Krp/Kad est également bien conservé, allant de 5,08 et 5,36. Enfin, le rapport des vitesses de chute des particules est beaucoup moins dispersé que pour l'exp. C : toutes les valeurs sont confinées entre 48,00 et 98,83. Notons que cet intervalle est inclus dans celui défini par l'exp. B2.

Cette expérience met en évidence la sensibilité du domaine acceptable trouvé lors de l'exp. C vis-à-vis des erreurs sur les données assimilées. Cependant, les rapports des paramètres s'avèrent robustes. Bien que préliminaire, cette analyse suggère que la solution C1 permet d'identifier un bassin acceptable robuste vis-à-vis des erreurs sur les données assimilées.

8.3.3 Robustesse des solutions vis-à-vis des erreurs sur les conditions aux limites

(a) Perturbation des conditions aux limites

Pour analyser la robustesse des solutions de l'exp. C vis-à-vis sur des erreurs des conditions aux limites, nous avons perturbé les conditions aux limites à l'intérieur de leurs barres d'erreurs en fonction de leur qualité a priori (section 7.2).

Nous avons ensuite réalisé une inversion exactement identique à l'exp. C, mis à part que les conditions aux limites utilisées pour intégrer le modèle sont les conditions aux limites perturbées.

(b) Expérience E : inversion à partir des conditions aux limites perturbées

L'AG a évalué 200 générations (i.e. 1000 valeurs du coût) avant de s'arrêter. Il a identifié 85 vecteurs de paramètres acceptables, dont le coût varie entre 0,99 et 0,65 (Figure 45). Aucun de ces vecteurs ne correspond exactement à ceux qui ont été détectés lors de l'exp. C. Comme pour l'exp. D, on note par rapport à l'exp. C une diminution de la dispersion des valeurs de Kdes, Kag, Kad et dans une moindre mesure de Vp. Les valeurs de Kdes, Kad, Krp et Kz de cette expérience sont très proches de celles de l'exp. D. Il semblerait que certains bassins identifiés par l'exp. D aient été retrouvés lors de l'exp. E. Parmis ceux-ci figurerait le bassin de la solution C1 (Tableau 18). Cela suggère que cette solution appartient à un bassin également robuste vis-à-vis des erreurs des conditions aux limites.

Les rapports Kdes/Kag', Krp/Krg et Krp/Kad calculés à partir des solutions de l'exp. E se trouvent dans les mêmes gammes de valeurs que ceux calculés pour l'exp. C (Figure 51, Tableau 19). Le rapport Kdes/Kag' varie entre 0,95 et 1,37. Les valeurs de Krp/Krg sont beaucoup moins dispersées que pour les exps. C et D et sont confinées entre 1,01 et 6,05. Le rapport Krp/Kad est compris entre 4,94 et 6,27. Le rapport des vitesses Vg/Vp varie entre 15,81 et 115,45. Cet intervalle est cohérent avec ceux délimités par les exps. B2 et D. Enfin, les quatre rapports associés à la solution C1 appartiennent aux intervalles délimités par l'exp. E.

Cette expérience démontre que le domaine acceptable délimité par l'exp. C est sensible aux erreurs sur les conditions aux limites. On constate à nouveau que les rapports des paramètres sont plus robustes que les valeurs individuelles des paramètres. Cette analyse de robustesse qualitative suggère que la solution C1 appartient à un bassin acceptable robuste vis-à-vis des erreurs sur les données in situ assimilées et utilisées comme conditions aux limites. Il est important de souligner que si cette solution paraît marginale relativement aux autres solutions acceptables de l'exp. C sur la Figure 45, elle n'en est pas pour autant moins probable. Sa "marginalité" apparente signifie simplement que l'AG a visité rapidement le bassin acceptable dans lequel elle se trouve.

8.4 Conclusion du chapitre

Dans ce chapitre, nous avons présenté six expériences d'inversion du modèle COLDO, avec l'objectif d'estimer les paramètres contrôlant les flux d'Al dans la colonne d'eau au site EUMELI oligotrophe. Nous avons démontré que l'AG sélectionné dans le Chapitre 6 permet de trouver des vecteurs de paramètres qui expliquent correctement - i.e. relativement aux barres d'erreur - les mesures in situ. Pour cela, il est nécessaire :

Nous avons montré que les solutions au problème inverse sont nombreuses, et proposé de réduire leur nombre en raffinant le critère de sélection. Ainsi, nous avons sélectionné un vecteur de paramètres par une analyse préliminaire et qualitative de la robustesse des solutions vis-à-vis des erreurs sur les données in situ.

Le Chapitre 9 consiste en une synthèse des résultats de ces expériences. Nous utiliserons ces conclusions pour appliquer cette approche à l'étude d'autres traceurs aux sites EUMELI oligotrophe et mésotrophe dans la Partie IV.


Chapitre 9 Récapitulation des résultats

Ce chapitre a pour but de synthétiser les résultats des expériences décrites dans le Chapitre 8. Il s'agit :

9.1 Evaluation de la méthode inverse

9.1.1 Performances et limites de l'algorithme génétique

Les expériences du Chapitre 8 démontrent que notre méthode inverse basée sur l'AG de Carroll (1996) permet d'identifier des vecteurs de paramètres expliquant l'évolution temporelle de la distribution de l'Al au site O, selon le schéma conceptuel du modèle non-linéaire COLDO (section 3.1). L'AG a toujours réussi à trouver plusieurs vecteurs de paramètres, et il n'a jamais été piégé par un minimum local non-acceptable. Cela confirme l'adéquation de cet algorithme pour l'exploration des fonctions coût complexes associées à notre problème inverse, ainsi que la robustesse de ses paramètres algorithmiques (section 6.3.3).

Cependant, l'assimilation de données in situ caractérisées par des incertitudes relativement élevées fait surgir des difficultés qui étaient inexistentes lors de l'assimilation de pseudo-données non bruitées (section 6.2). La résolution complète du problème inverse exige de trouver l'ensemble des vecteurs acceptables dont le coût est inférieur ou égal à 1 (section 8.1.2(a)). Les figures 45 et 48 montrent que les domaines acceptables associés aux différentes expériences inverses sont très vastes relativement aux gammes des valeurs possibles des paramètres (Tableau 18). En outre, leur structure semble très complexe : ils paraissent tous être formés de plusieurs bassins disjoints. Cela implique qu'à la différence des problèmes inverses linéaires, il n'est pas toujours possible de passer de façon continue d'une solution acceptable à une autre.

Or l'AG a été conçu pour rapidement localiser le MG de fonctions de plusieurs variables ayant des minima locaux, et non pour délimiter des isocontours de ces fonctions. Il n'a pas non plus été développé pour nécessairement passer par des bassins acceptables lors de son trajet vers le MG. La configuration de cet AG permet donc de repérer uniquement les quelques vecteurs de paramètres détectés de façon quasi-aléatoire au cours de la minimisation de la fonction coût. Leur nombre dépend du critère d'arrêt de l'algorithme défini empiriquement (section 7.3.2).

9.1.2 Perspectives

A notre connaissance, il n'existe pas d'algorithme permettant de résoudre complètement le problème inverse auquel nous avons à faire. Comme nous l'avons mentionné à l'issue de l'expérience inverse simulée (exp. B1, section 8.1.2(a)), la résolution du problème peut être améliorée en appliquant deux stratégies complémentaires.

(a) Amélioration de l'algorithme génétique

La première stratégie consiste à modifier l'AG de façon à augmenter la probabilité qu'il détecte des vecteurs de paramètres acceptables. Deux améliorations sont envisageables à court terme :

A plus long terme, d'autres améliorations sont envisageables en collaboration avec les chercheurs qui développent ces algorithmes. Leur aide nous est indispensable pour évaluer la compatibilité ainsi que les avantages et les inconvénients des différents algorithmes évolutifs (Bäck, 1996; Bäck et Schwefel, 1996; Schoenauer et Michalewicz, 1997) et de leurs configurations variées. Par exemple, il est impossible de simuler la notion de niche écologique avec les algorithmes de stratégies évolutives évoqués dans la section 6.3.3 (M. Schoenauer, communication personnelle, 2000). Cette notion est aussi incompatible avec la configuration du "micro-AG" puisqu'elle exige des tailles de population classiques (i.e. 100 à 200 individus ; D. Carroll, communication personnelle, 2001).

(b) Raffinement du critère de sélection

L'autre stratégie consiste à réduire la taille du domaine acceptable, en raffinant judicieusement le critère de sélection des paramètres. Le critère de sélection de départ est basé sur l'écart entre les mesures in situ et les simulations générées par COLDO (section 7.1).

Couplage à des méthodes robustes

Dans la section 8.3, nous avons proposé d'ajouter des critères de sélection a posteriori basés sur la robustesse des solutions vis-à-vis des incertitudes sur le modèle et sur les données. Nous avons analysé de façon très préliminaire la sensibilité des solutions inverses de l'exp. C par rapport à la paramétrisation de l'agrégation des particules filtrées (section 8.3.1). Les résultats suggèrent que la stabilité structurale de COLDO est trop faible pour que l'on puisse identifier des solutions robustes vis-à-vis de la paramétrisation des processus. Les résultats de l'analyse - toujours préliminaire - de la sensiblité des solutions par rapport aux erreurs sur les données assimilées (section 8.3.2) et sur les conditions aux limites (section 8.3.3) indiquent que ces critères de robustesse permettent de réduire le nombre de solutions admissibles. Cette analyse a conduit à identifier une solution robuste désignée par "solution C1" (Tableau 18 ; Figure 52).

Le couplage de l'AG à des analyses de robustesse semble être une approche très prometteuse. A l'avenir, des efforts devront donc être consacrés :

Adoption d'une approche "multi-proxies"

Nous montrerons dans le Chapitre 11 que l'on peut raffiner le critère de sélection des paramètres en assimilant indépendemment ou simultanément les mesures in situ de plusieurs traceurs collectées sur un même site.


(c) Etude de l'identifiabilité des paramètres

La taille du domaine acceptable pourrait être réduite en analysant l'identifiabilité structurelle des paramètres lors du développement du modèle. Il s'agit de vérifier que chaque trajectoire du modèle ne peut être générée que par un seul vecteur p (section 8.1.2(a)). Les méthodes proposées par Walter et Pronzato (1993, 1994) sont adaptées aux modèles dynamiques basés sur des EDO, c'est-à-dire sans dimension spatiale. Des efforts devraient également être consacrés à l'adaptation de ces méthodes aux modèles basés sur des systèmes d'EDP.

Symbole

Solution C1

Solution C2

Solution C3

Solution C4

Paramètres biogéochimiques

Kdes (/j)

0,5404

1,0539

0,9861

0,9850

Kag (m3/mg/j)

0,0971

0,2071

0,2079

0,2140

Kad (/j)

0,0503

0,0501

0,0614

0,0461

Krp (/j)

0,2508

0,2510

0,3344

0,2510

Krg (/j)

0,2098

0,0095

0,1871

0,0980

Paramètres physiques

Vp (m/j)

8,90

0,08

6,61

0,31

Vg (m/j)

776,54

751,51

662,36

662,36

Kz (m2/j)

50,08

53,94

48,15

48,15

Tableau 20. Valeurs des paramètres pour quatre des solutions de l'exp. C (Tableau 17, Figures 45 et 51).

(d) Exploitation des solutions inverses

La très forte sensibilité de la dynamique du modèle et par conséquent des solutions inverses vis-à-vis de la paramétrisation des processus – par définition empirique – limitent l'usage des résultats. Par exemple, la solution C1 que nous avons sélectionnée dans la section 8.3 peut générer des simulations irréalistes si elle est utilisée avec un autre modèle que COLDO, même si leurs équations ne diffèrent que légèrement (section 8.2.2). Il est très probable également que cette solution produise de mauvais résultats avec un modèle biogéochimique 3-D de l'océan (Evans, 1999). La faible stabilité structurelle est une caractéristique très générale des modèles biogéochimiques. L'intérêt des solutions inverses pourrait être accru si l'on encourageait le développement de modèles structurellement stables (Wiggins, 1990).

Etant donnée la forte variabilité des processus dans la colonne d'eau en fonction des environnements biologiques et physiques (Bishop, 1989), les solutions telles que la solution C1 doivent être utilisées avec prudence pour simuler les flux d'Al dans d'autres régions de l'océan. Par contre, notre approche se révèle adaptée à la quantification des flux associés à la distribution d'un traceur donné.


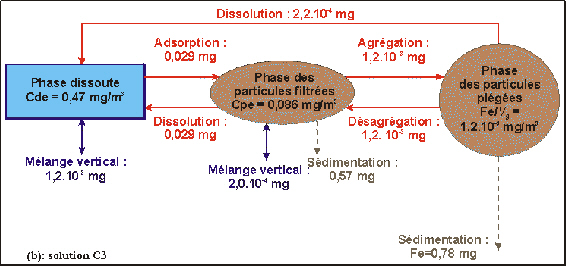
Figure 53. Distribution de l'Al dans 1 m3 d'eau de mer à 2500 m au site EUMELI oligotrophe le 1er décembre 1991 calculée par les solutions C1 (a), C3 (b), et C4 (c). Les quantités d'Al échangées entre les phases au cours de dt = 1 j sont indiquées en rouge. Celles qui sont échangées avec la colonne d'eau sous- ou sus-jacente par mélange vertical pendant dt = 1 j sont indiquées en bleu. Enfin, les quantités d'Al particulaire qui ont traversé le volume de 1 m3 pendant cette même durée sont indiquées en marron. Pour la clarté des schémas, les grandeurs sont fournies avec deux chiffres significatifs. Les paramètres associés à chaque solution sont donnés dans le Tableau 20.

Figure 53 (suite)

9.2 Extraction des résultats géochimiques

Cette section a pour but d'identifier les informations apportées par les expériences inverses du Chapitre 8 – en particulier par l'exp. C (section 8.2.2) - sur les flux associés au transfert vertical de l'Al dans la colonne d'eau au site O. Ces informations doivent être considérées avec précaution. En effet, elles sont basées sur les quelques solutions acceptables trouvées par l'AG au cours de la minimisation de la fonction coût. En outre, elles dépendent des hypothèses que nous avons dû faire à cause du manque d'information sur les corrélations temporelles entre les erreurs sur les données (section 7.1.1) ainsi que du manque de données in situ (section 7.2).

9.2.1 Quantification des flux d'Al dans la colonne d'eau au site oligotrophe

L'intérêt majeur des solutions inverses réside dans la possibilité de quantifier les flux d'Al résultant de la sédimentation des particules, ceux qui sont échangés entre les phases dissoute, filtrée et piégée, et ceux qui sont liés au mélange vertical de la colonne d'eau. La Figure 53 montre la distribution et les flux d'Al à 2500 m au site O calculés par trois solutions de l'exp. C semblant appartenir à trois bassins acceptables distincts (Figures 45 et 51 ; Tableau 20). Les résultats sont présentés de façon complémentaire sur les figures 54 à 56.

En accord avec les mesures assimilées, le principal réservoir d'Al est la phase dissoute (Figure 53). Les vitesses de chute des particules piégées associées aux trois solutions (Vg = 776,54 m/j pour la solution C1 et Vg = 662,36 m/j pour les solutions C3 et C4, cf. Tableau 20) impliquent que la concentration en Al est minimale dans la phase piégée. Les trois solutions montrent la prédominance des flux d'Al résultant de la sédimentation des particules par rapport aux flux échangés entre les phases, et au flux lié au mélange vertical de la colonne d'eau (Figure 53). La solution C1, qui semble plus robuste que les deux autres vis-à-vis des erreurs sur les données in situ (section 8.3) prédit que les particules filtrées sont les principales responsables du transport de l'Al vers le sédiment. Ce résultat est cependant très sensible à la valeur de Vp (Figure 53 ; Vp = 8,90 m/j, Vp = 6,61 m/j et Vp = 0,31 m/j pour les solutions C1, C3 et C4 respectivement, cf. Tableau 20).

Les figures 54 à 56 montrent que les effets de l'agrégation et de la désagrégation sur le flux de masse sont du même ordre de grandeur sur toute la durée de la campagne. Ce résultat, prévisible à partir des valeurs du rapport Kdes/Kag' associées aux solutions de l'exp. C (Figure 51 ; Tableau 19), confirme a posteriori la nécessité de paramétriser l'influence de l'agrégation des particules filtrées sur le flux de masse (section 8.2.1). La diminution du flux de masse avec la profondeur serait liée à la légère supériorité de la désagrégation par rapport à l'agrégation (Figures 54 à 56).

La diminution du flux d'Al résulterait principalement de la désagrégation des particules piégées, et dans une moindre mesure de la dissolution de l'Al piégé (Figures 53 à 56 ). Ce résultat est compatible avec la prédominance de la fraction lithogénique de l'Al particulaire dans l'océan et avec le comportement réfractaire de celle-ci (Jickells, 1995; cf. section 10.2.1). La Figure 53 montre cependant que ~10 à 18 % de l'Al piégé se dissout. Ces valeurs sont en contradiction avec les résultats expérimentaux de Arraes-Mescoff et al. (2001) qui ne montrent pas de dissolution significative de l'Al fixé sur les particules mises à incuber. Les échanges d'Al entre les phases concernent essentiellement les phases dissoute et filtrée. Les trois solutions montrent que le piégeage de l'Al par la phase filtrée serait réversible, et que ~25 à 34 % de l'Al filtré pourrait se dissoudre (Figure 53). Les fractions de l'Al filtré et piégé correspondent a priori à de l'Al biogénique (MacKenzie et al., 1978; Van Beusekom, 1988 ; cf. section 10.2.1) puisque les expériences in vitro montrent que l'Al lithogénique est insoluble (Arraes-Mescoff et al., 2001). Cependant, de nombreuses études de la distribution dans la colonne d'eau d’éléments peu solubles ou insolubles montrent qu'elle ne peut être expliquée sans faire l'hypothèse d'un échange réversible entre les phases dissoute et filtrée. Ainsi, cet échange est nécessaire pour expliquer les profils des rapports d'activité du 230Th et du 232Th entre les phases dissoute et particulaire (Roy-Barman et al., 1996). Il permet aussi d'interpréter les profils de la composition isotopique de ces deux phases, et les spectres de terres rares des particules en suspension (Tachikawa, 1997; Tachikawa et al., 1999, 2001). Les dispositifs actuels des expériences in vitro ne permettent pas d'identifier la nature de ce mécanisme d'échange réversible. Les flux d'Al par adsorption seraient exactement compensés par la dissolution de l'Al particulaire filtré (Figures 53 à 56). Cette compensation est également déductible à partir des valeurs du rapport Krp/Kad trouvées pour l'exp. C (Figure 51 ; Tableau 19). En effet, Krp/Kad ~5, et l'assimilation maintient le rapport Cpe/Cde à ~0,2, ce qui conduit à 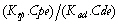~1. Cette compensation et la faible dissolution de l'Al piégé (Figures 54 à 56) expliquent la faible variabilité temporelle des profils simulés de Cde (Figure 52).

D'après les simulations que nous avons faites à 1500 et 3500 m avec les mêmes solutions acceptables, l'importance relative des phases et des flux d'Al décrite ci-dessus est indépendante de la profondeur et du temps.

Figure 54. Contributions des termes de la nouvelle version de COLDO (Eqs. 25 et 3 à 5) à la variabilité temporelle de Fm, Fe, Cpe et Cde à 2500 m calculées par la solution C1 (Figures 45 et 51 ; Tableau 20).

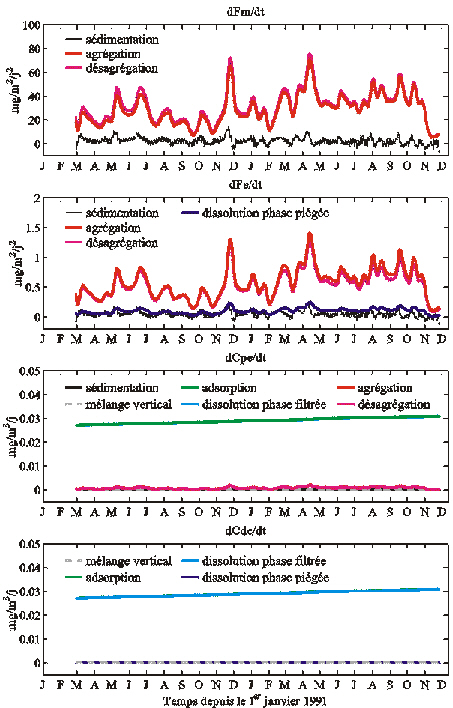
Figure 55. Contributions des termes de la nouvelle version de COLDO (Eqs. 25 et 3 à 5) à la variabilité temporelle de Fm, Fe, Cpe et Cde à 2500 m calculées par la solution C3 (Figures 45 et 51 ; Tableau 20).

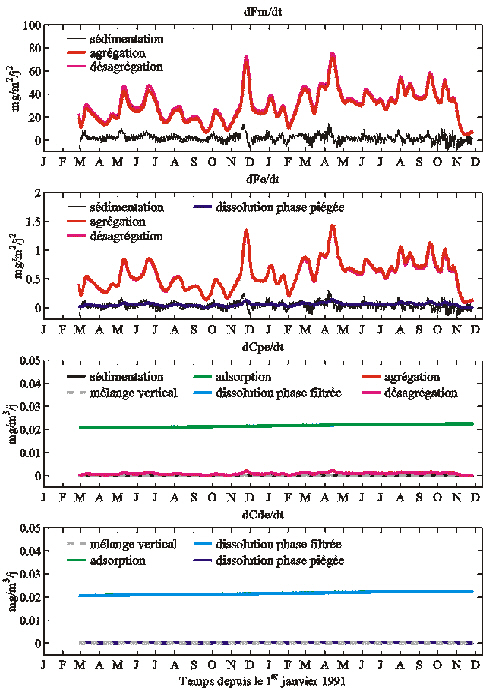
Figure 56. Contributions des termes de la nouvelle version de COLDO (Eqs. 25 et 3 à 5) à la variabilité temporelle de Fm, Fe, Cpe et Cde à 2500 m calculées par la solution C4 (Figures 45 et 51 ; Tableau 20).

9.2.2 Interprétation de la vitesse de chute des particules piégées

Les valeurs des vitesses de chute de la plupart des solutions de l'exp. C sont comprises entre 600 et 800 m/j (Figure 45) : elles sont plus de trois fois supérieures aux valeurs classiquement admises pour les régions oligotrophes (~100-200 m/j ; cf. Deuser et al., 1990; Asper et al., 1992; Newton et al., 1994; Khripounoff et al., 1998; Bory et Newton, 2000). Ces fortes valeurs sont pourtant nécessaires pour reproduire la simultanéité – relativement à la période de collecte des pièges – des évènements de flux élevés à 2500 et 4400 m à l'aide de COLDO (Figure 43). Cela s'explique très probablement par le fait que le modèle ne décrit pas explicitement l'influence de la dissolution des éléments majeurs sur la diminution du flux de masse avec la profondeur. Mais il faut également souligner que la plupart des valeurs reportées dans la littérature sous-estiment les vitesses de chute réelles, car elles sont évaluées à partir du décalage temporel entre les évènements enregistrés par des pièges fixés à des profondeurs différentes. Ces pièges enregistrent le flux moyen sur la période de collecte, celle-ci pouvant varier entre quelques jours et quelques mois (section 2.2.2(a)). Par conséquent, ces estimations sont des valeurs minimales. En outre, des expériences in vitro (Takahashi et Bé, 1984) et des expériences de modélisation (Bijma et al., 1994) montrent que des tests de foraminifères tels que ceux que l'on a retrouvés dans les godets des pièges à EUMELI (K. Tachikawa, communication personnelle, 2000) peuvent sédimenter à des vitesses allant de 100 à 5000 m/j selon leur taille.

9.2.3 Variabilité spatio-temporelle des processus dans la colonne d'eau

Dans la mesure où les paramètres de COLDO sont indépendants du temps et de la profondeur, l'assimilation ajuste le modèle au comportement dominant de la colonne d'eau réflété par les données in situ. La variabilité temporelle et spatiale de cet ajustement, que l'on a décrite en particulier pour les simulations de la solution C1 démontre que le mode de fonctionnement de la colonne d'eau, et par conséquent les paramètres, varient avec la profondeur et le temps (Figure 52, section 8.2.2). La prise en compte de ces variabilités dans le modèle rendrait le problème inverse extrêmement complexe. Dans la section 12.2.2(b), nous montrerons comment contraindre indirectement la variabilité temporelle des paramètres.

9.3 Suggestions de stratégies d'échantillonnage de la colonne d'eau

Comme nous l'avons mentionné dans la section 4.2.3, il est difficile de quantifier la durée et les fréquences temporelles et spatiales d'échantillonnage permettant d'estimer les paramètres d'un système non-linéaire, surtout lorsqu'on dispose au départ de peu de données in situ. Il n'est pas aisé non plus de définir le nombre de variables à mesurer. Cependant, notre approche permet de suggérer des stratégies de mesure pour raffiner le critère de sélection, et par conséquent améliorer les solutions inverses.

En supposant que le modèle est correct, la comparaison des exps. A et B2 (sections 8.1.1 et 8.1.2(b)) montre que le couplage non-linéaire entre les trois phases est trop faible pour que l'échantillonnage de l'une d’entre elles permette de contraindre les deux autres. Cela signifie que l'estimation des paramètres contrôlant la distribution dans la colonne d'eau d’un traceur tel que l'Al exige de mesurer les trois phases sur un même site, à des dates et à des profondeurs cohérentes entre elles. Les fréquences d'échantillonnage doivent être cohérentes avec la variabilité spatio-temporelle a priori de chaque phase. Cette exigence a déjà été exprimée à la suite d'analyses plus qualitatives de mesures in situ, en particulier par Jeandel et al. (1995) et Bacon et al. (1996), mais elle n'est encore que peu appliquée à l'heure actuelle.

L'échantillonnage des particules piégées exige de positionner au moins trois pièges dans la colonne d'eau. Le piège superficiel permet le calcul des conditions aux limites, et les deux autres servent à évaluer la capacité du modèle à reproduire le transfert vertical de la matière. En outre, la concentration du traceur considéré sur les particules piégées doit être mesurée pour tous les pièges. Dans la mesure où il est nécessaire de prendre en compte l'effet de l'agrégation des particules filtrées sur le flux de masse (section 8.2 ; Arraes-Mescoff, 2000; Roy-Barman et al., 2001), l'échantillonnage de la phase filtrée doit inclure la mesure de la concentration totale en particules filtrées.

Les exps. B2, C, D et E (Tableau 17) montrent que même lorque toute la base de données est assimilée, certains paramètres tels que Krg, Vp et Vg sont mal contraints (Figure 45). La robustesse des rapports Kdes/Kag', Krp/Krg et Krp/Kad associés à leurs solutions implique l'existence de dégénérescences du coût rectilignes (Figure 51). La combinaison des robustesses des rapports Krp/Krg et Krp/Kad suggère que l'une d’elle concerne 3 des Np = 8 dimensions de l'espace des paramètres. Comme nous l'avons indiqué dans la section 4.2.3, la diversification des types d'observations, c'est-à-dire l'utilisation de nouveaux instruments de mesure permettrait de réduire la sous-détermination du problème. Par exemple, le profileur vidéo marin (Stemman et al., 2000) et les appareils optiques (Claustre et al., 2000) apportent des informations sur le système particulaire qui sont complémentaires de celles fournies par les pièges, les pompes et les bouteilles (section 2.2.2(d)). Pour illustrer cette remarque, la Figure 57 représente les simulations calculées à partir de la solution C2 (Figure 45 ; Tableau 20). Elles sont cohérentes avec les données, mais l'analyse des profils de Fm et Fe révèle des structures verticales à petite échelle (~100 m) qui ne peuvent pas être observées par les pièges à particules (Figure 58 : dans le cas présent, ces structures correspondent vraisemblablement à un artefact lié à la méthode d'intégration puisque leur dimension est égale au pas vertical du modèle : dz = 100 m). Par contre, les profils de Fm et Fe simulés par les solutions C1, C3 et C4 (Tableau 20) montrent une faible variabilité verticale. La réalisation de quelques profils de la distribution des particules à haute résolution, par exemple avec le profileur vidéo sous-marin, compenserait la faible résolution des pièges à particules et permettrait de distinguer les deux groupes de solutions.

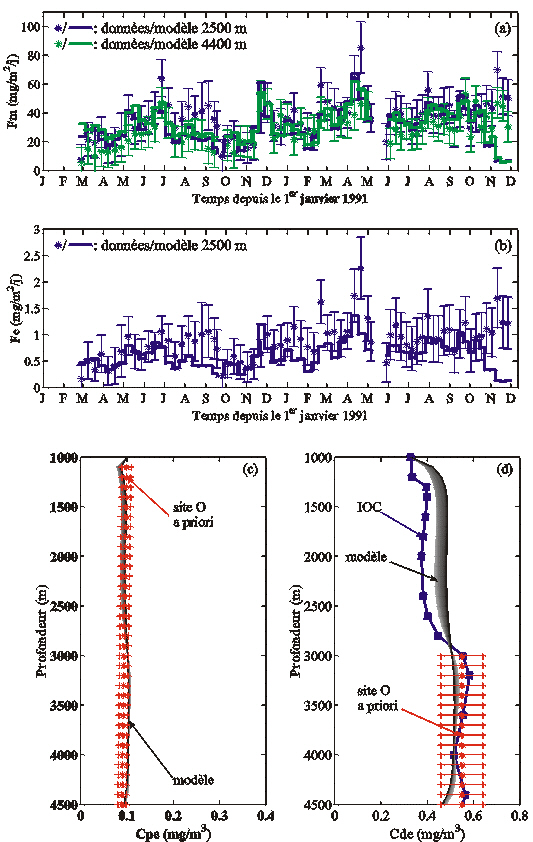
Figure 57. Flux de masse (a), d'Al (b), Al particulaire (c) et dissous (d) simulés par la solution acceptable C2 trouvée lors de l'exp. C (section 8.2.2; Tableau 20). Les simulations sont comparées aux mesures des pièges à particules et aux profils calculés pour les phases filtrée et dissoute qui ont tous été assimilés. Les profils simulés de Cpe et Cde sont d'autant plus récents qu'ils sont sombres.

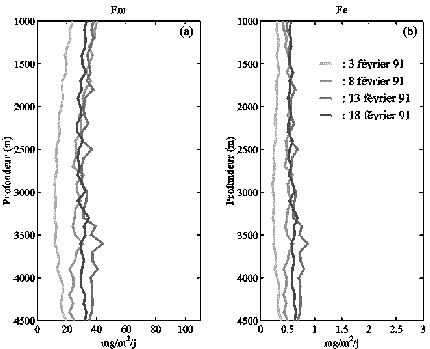
Figure 58. Profils des flux de masse (a) et d'Al (b) simulés à partir de la solution C2 (Figure 45 ; Tableau 20). Ils montrent des structures verticales de petite échelle (~ 100 m). Elles ne sont pas observables à partir des pièges à particules, mais il serait possible de vérifier leur existence à des profondeurs inférieures à 1000 m à partir du profileur vidéo sous-marin (section 2.2.2(d)).

Les expériences du Chapitre 8 démontrent la forte influence des erreurs des données in situ sur les solutions inverses : elles contrôlent en partie la taille et les limites du domaine acceptable (Figures 41 et 42). Par conséquent, il est essentiel d'estimer aussi précisément que possible les erreurs de collecte ainsi que les erreurs analytiques. En particulier, les stratégies de mesure doivent inclure une évaluation systématique de l'efficacité de tous les pièges à particules, à partir de l'échantillonnage des couples isotopiques indiqués dans le Tableau 1 (Bacon, 1996). La connaissance de l'efficacité des pièges permettrait en outre de corriger les mesures et de ne pas forcer les modèles à reproduire les variations spatio-temporelles des flux résultant d'artefacts (Scholten et al., 2001). Qu'elles soient sauvergardées dans une base de données ou publiées, les mesures doivent systématiquement être fournies avec leurs barres d'erreur. Une meilleure connaissance des erreurs sur les mesures faciliterait également la définition des termes de corrélation temporelle entre les erreurs dans la fonction coût (Eq. 23).

Le contexte le plus approprié pour appliquer et poursuivre le développement de cette approche inverse serait une station où l'approximation unidimensionnelle est réaliste et qui serait échantillonnée sur le long terme (i.e. plusieurs années) par des instruments de mesure variés. La station DYFAMED située en Mer Ligure en est un très bon exemple (Marty, 1993). En effet, l'augmentation de la durée totale d'échantillonnage accroît la résolution du coût dans l'espace des paramètres (section 4.2.3). Les stations longues sont propices à l'étude de l'influence des résolutions d'échantillonnage sur l'estimation des paramètres. Elles favorisent aussi l'analyse des relations entre les fréquences d'échantillonnage et les échelles de temps caractéristiques des principaux forçages externes. Des expériences in vitro menées parallèlement à ces études in situ contribueraient à améliorer la paramétrisation des processus.

9.4 Conclusion du chapitre

La synthèse des résultats des expériences inverses réalisées dans cette troisième partie montre que nous devons améliorer l'AG pour le rendre mieux adapté à l'assimilation des données in situ. En parallèle, il est nécessaire de réduire le nombre de solutions inverses admissibles. Ceci exige :

Les améliorations de la méthode ne seront envisagées qu'à la suite du travail présenté dans ce manuscrit.

L'intérêt des solutions inverses réside dans la possibilité de quantifier de l'importance relative des processus dans la colonne d'eau, et lorsqu'une solution peut-être sélectionnée, dans la quantification des flux d'un traceur donné dans la colonne d'eau et entre les phases dissoute, filtrée et piégée. La quantification des flux d'Al au site EUMELI oligotrophe présentée dans ce chapitre est cohérente avec les résultats obtenus antérieurement sur le comportement de cet élément dans l'océan (section 10.2.1).

Dans la dernière partie, nous allons inverser COLDO avec des mesures d'autres traceurs collectées aux sites EUMELI oligotrophe et mésotrophe. En confrontant l'ensemble des résultats géochimiques obtenus, nous essaierons de décrire et comparer le fonctionnement de la colonne d'eau à ces deux sites.

Back | Next

Titre: Thèse de Véronique Athias-Lefèvre
Version: 1
Date: 21 août 2001