UNIVERSITÉ TOULOUSE III - PAUL SABATIER
THESE
Pour obtenir le grade de
DOCTEUR DE L’UNIVERSITÉ TOULOUSE III
Discipline : Biogéochimie marine
présentée par
Véronique ATHIAS
Ancienne élève de l’Ecole Normale Supérieure de Lyon
Titre :
UNE MÉTHODE D’ESTIMATION PARAMÉTRIQUE NON-LINÉAIRE POUR MODÉLISER LES FLUX DE MATIÈRE DANS LA COLONNE D’EAU OCÉANIQUE
Application à l’Océan Atlantique tropical nord-est
(sites EUMELI)
_________
Directeurs de thèse :
Catherine JEANDEL et Pierre MAZZEGA
Date de soutenance : 21 juin 2001
_________
JURY
| Robert ROSSET | Président |
| Laurent MÉMERY | Rapporteur |
| Olivier TALAGRAND | Rapporteur |
| Catherine JEANDEL | Directrice de thèse |
| Pierre MAZZEGA | Directeur de thèse |
| Olivier BERNARD | Rapporteur |
| Gérald DESROZIERS | Examinateur |
| Christiane Lancelot | Examinatrice |
Remerciements
Catherine et Pierre, je vous remercie d’avoir eu l’idée géniale de définir ensemble un sujet de thèse aussi passionnant. Cela tient sans nul doute à votre grande ouverture d’esprit, et c’est une qualité fort appréciable…. Je vous suis également reconnaissante de m’avoir fait profiter de toutes vos connaissances. J’ai énormément apprécié votre disponibilité, votre patience ainsi que la confiance que vous m’avez accordée pour mener à bien ce travail de façon autonome et indépendante. Au-delà de vous deux, je remercie toute l’équipe de géochimie marine du LEGOS, c’est-à-dire Kazuyo, Roséana, Fredo., François, Marc, Matthieu et Laurent, pour leur agréable compagnie et pour m’avoir aidée à comprendre les trucs et astuces de leurs recettes de cuisines et autres manipulations expérimentales
…Je voudrais remercier très chaleureusement Christiane Lancelot pour m’avoir accueillie pendant deux mois dans son laboratoire à Bruxelles. Sa grande sagacité et sa bienveillance m’ont beaucoup apporté. J’ai beaucoup appris de mon séjour en Belgique, grâce aux nombreuses discussions que j’ai eu avec les différentes personnes de son laboratoire, l’ESA, toutes très disponibles. J’adresse aussi mes remerciements à Jim Gunson, Geoff Evans, Markus Schartau, Marc Schoenauer et à Olivier Bernard pour leurs critiques judicieuses et leurs conseils avisés au sujet de mon travail. Je remercie également Francis Albarède pour m’avoir largement aidée à faire mes premiers pas dans le domaine de l’océanographie, et pour avoir soutenu mon travail dès le départ, lorsque d’autres semblaient beaucoup plus perplexes quant à l’intérêt de mes travaux.
Robert Rosset est remercié pour avoir accepté de présider le jury de ma thèse. Mes plus vifs remerciements vont à mes rapporteurs, Laurent Mémery et Olivier Talagrand, dont les questions, remarques, critiques et commentaires m’ont permis de prendre du recul par rapport à mon travail. Merci également à Gérald Desroziers pour l’intérêt qu’il a porté à mon travail.
J’adresse également mes remerciements à tous les thésards que j’ai côtoyés au LEGOS, et en particulier à Loren Carrère avec qui j’ai partagé mon bureau. Merci à Martine Ména et Nadine Lacroux pour leur soutien.
Merci également à ma petite famille et à mes amis grimpeurs, plongeurs, randonneurs et doux rêveurs pour m’avoir encouragée et/ou soutenue tout au long de ces longues études
…Enfin, merci à toi Fabien, pour ta grande patience vis-à-vis de mes humeurs diverses et variées au cours de la maturation de ce travail
…Sommaire
Table des illustrations
Figure 1. Les échanges de matière entre l’océan et les grands réservoirs terrestres (extrait de Brown et al., 1992)
Figure 2. Origine et distribution des particules marines (d’après Jeandel, 1998)
Figure 3. Les principaux instruments de mesure des flux dans la colonne d’eau
Figure 4. Piège à particules conique Technicap PPS5 de 1 m de diamètre dans le port de Monaco (http://www.iaea.org/monaco/news.html)
Figure 5. Pompe in situ le long d’un câble du navire océanographique Le Marion Dufresne, lors de la campagne Antarès IV (http://www.iaea.org/monaco/news.html)
Figure 6. Rosette de bouteilles Niskin (http://www.pmel.noaa.gov/epic/ctd/profile-help.html)
Figure 7. Profileur Vidéo Marin développé par G. Gorsky en 1992 (http://www.obs-vlfr.fr/~pvm/)
Figure 8. Localisation des sites EUMELI dans le contexte hydrologique régional. CC: Courant des Canaries; NASG: Gyre Subtropicale Nord Atlantique; NECC: Contre-Courant Nord Equatorial; NEC: Courant Nord Equatorial; MU: Upwelling Mauritanien.
Figure 9. Stratification des masses d’eau et circulation océanique le long de la marge continentale africaine nord-ouest (extraite de Sarthein et al., 1982). AABW: eau de fond antarctique; CC: courant des Canaries; EUC: sous-courant équatorial; GW: courant de Guinée; MOW: eau méditerranéenne; NACW: eau centrale nord-atlantique; NADW: eau profonde nord atlantique; SACW: eau centrale sud atlantique; SAIW: eau intermédiaire sud atlantique; SW: eau de surface
Figure 10. Champs de vents zonaux moyens dans la couche comprise entre 0 et 400 m au-dessus de l’Atlantique Nord tropical en janvier (a) et juillet (b; extraite de Chiapello et al., 1995)
Figure 11. Carte composite de concentrations moyennes en chlorophylle a pour le mois de janvier dans l’Atlantique Nord mesurées par l’instrument SeaWIFS (Sea-viewing WIde Field-of-view Sensor ) opérationnel depuis septembre 1997 (http://daac.gsfc.nasa.gov/CAMPAIGN_DOCS-/OCDST/ocdst_north_atlantic_productivity.html)
Figure 12. Carte globale de la distribution des aérosols réalisée à partir des mesures de l’instrument POLDER porté par le satellite ADEOS du CNES (http://wwwprojet.cst.cnes.fr:8060/POLDER/SCIEPROD/ae9706.htm)
Figure 13. Echantillonnage des pièges à particules au site O. Les triangles symbolisent la date d’immersion des pièges, et les tirets la durée d’échantillonnage pour chacun des trois déploiements (Tableau 4). Les échantillons des pièges représentés en couleur (1000, 2500 et 4400 m) sont exploitables; ceux des pièges représentés en noir (250 et 4590 m) ne le sont pas.
Figure 14. Echantillonnage des pièges à particules au site M. Les triangles symbolisent la date d’immersion des pièges, et les tirets la durée d’échantillonnage pour chacun des trois déploiements (Tableau 5). Les échantillons des pièges représentés en couleur (1000, 2500 et 3000 m) sont exploitables; ceux du piège représenté en noir (250 m) ne le sont pas.
Figure 15. Flux de masse (a), de carbone organique (b) et d’aluminium (c) mesurés dans la colonne d’eau au site O
Figure 16. Flux de masse (a), de carbone organique(b) et d’aluminium (c) mesurés dans la colonne d’eau au site M
Figure 17. Schéma conceptuel du modèle COLDO.
Figure 18. Représentation de l’évolution temporelle (à gauche) et de l’attracteur (à droite) de systèmes de trois variables (x,y,z) caractérisés par trois comportements dynamiques distincts. (a): comportement périodique à une seule période ; (b): comportement quasi-périodique; (c): comportement chaotique associé au modèle de Lorenz (1963).
Figure 19. Variations du comportement de la solution à l’équation logistique non-linéaire (Eq. 6) lorsqu’on fait varier son unique paramètre a (May, 1976). Les cas représentés en noir, bleu, vert et rouge correspondent respectivement à a=2,6; a=3.414; a=3,845 et a=3,82.
Figure 20. Diagramme de bifurcation associé à l’équation logistique (Eq. 6) lorsque son unique paramètre a varie entre 2,5 et 4,0 (May, 1976). Les quatre valeurs utilisées pour réaliser la Figure 19 sont rappelées avec le même code de couleur.
Figure 21. Schéma réalisé d’après Menke (1989) sur la distinction entre l’approche directe (flèches vertes) et l’approche inverse (flèches rouges).
Figure 22. Un problème inverse classique: ajustement d’une droite (le “modèle”) à un ensemble d’observations. Le trait vert symbolise le calcul de la distance entre une observation yoi et la valeur prédite par le modèle, yi=a.xi+b.
Figure 23. Forme des fonctions coût associées aux cas 1 (a), 2 (b) et 3 (c) de l’Encadré 1. La forme discrétisée des modèles est intégrée sur 500 pas de temps Dt. La comparaison entre les trajectoires d’essai et la trajectoire optimale est faite à partir de t = 10.Dt, puis tous les 10.Dt.
Figure 24. Données in situ et simulations associées au transfert de l’Al au site EUMELI oligotrophe. Les données in situ (en rouge) sont utilisées pour définir les conditions initiales et les conditions aux limites. Les paramètres utilisés pour calculer les simulations à 2000 m (trait plein bleu) et 3000 m (trait plein vert) sont donnés dans le Tableau 13. Les symboles (carrés et triangles) représentent les pseudo-mesures échantillonnées à chaque profondeur.
Figure 25. Sections bidimensionnelles de la fonction coût calculée avec les pseudo-données représentées sur la Figure 24. Pour la première section (a en 2D et b en 3D), les valeurs de Kad, Krp, Krg, Vp, Vg et Kz sont les valeurs optimales (Tableau 13). Pour la deuxième section (c en 2D et d en 3D), la valeur de Kad est fixée à 4.10-3 /j. Les valeurs de Krp, Krg, Vp, Vg et Kz sont les valeurs optimales. Les abréviations sont : MG : Minimum Global, MS : Minimum Secondaire, et PS : Point de Selle.
Figure 26. Section bidimensionnelle de la fonction coût associée aux paramètres optimaux donnés dans le Tableau 13. Les valeurs de Kad, Krp, Krg, Vp, Vg et Kz sont les valeurs optimales. Les abréviations sont identiques à celles de la Figure 25.
Figure 27. Section bidimensionnelle de la fonction coût associée à un jeu de pseudo-données calculées avec COLDO et les paramètres optimaux donnés dans le Tableau 13. Les valeurs de Kad, Krp, Krg, Vp, Vg et Kz sont les valeurs optimales. Les abréviations sont identiques à celles de la Figure 25.
Figure 28. Minimisation par un algorithme de descente de gradient d’une fonction coût parabolique associée à un problème inverse linéaire. Kopt est la solution du problème inverse et les Kk sont les estimations successives de la solution.
Figure 29. La linéarisation d’un problème inverse non-linéaire conduit à minimiser les paraboles tangentes à J(K) au niveau des solutions a priori calculées successivement à partir de Kprior (d’après Menke (1989)).
Figure 30. Dans le cas où Kprior est trop éloigné de la solution Kopt, les minimisations successives des paraboles tangentes à J(K) peuvent conduire à un minimum local (d’après Menke (1989)).
Figure 31. Minimisation de la section du coût représentée sur la Figure 25a-b par l’algorithme du gradient conjugué non-linéaire de Fletcher-Reeves (Fletcher et Reeves, 1964; Gilbert et Nocedal, 1992). Le losange rouge indique le point de départ (i.e. pprior). Les points rouges symbolisent les mises à jour des solutions a priori, autour desquelles le problème est linéarisé. La minimisation s’achève sur le minimum secondaire (petite croix bleue) de la section, et non sur le minimum global (grande croix bleue). L’étoile bleue symbolise le point de selle.
Figure 32. Principe de la minimisation globale par le TRUST suivant 4 cycles ((a) à (d); extrait de Cétin et al., 1993). Sur ces schémas, f(x) et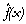 
correspondent respectivement à J(x) et 
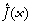mentionnées dans le texte. Le point de départ est x* = xL. Ensuite, x1*, x2* et x3* sont les minima locaux détectés successivement par le TRUST, qui sont utilisés pour définir les fonctions de subénergie Esub(x,x*), et sur lesquels sont définis les “repellers”. Enfin, xGM* est le minimum global.
Figure 33. Première minimisation de la section bidimensionnelle du coût par le TRUST. Il minimise la fonction j(a) obtenue en échantillonnant la section par une spirale d’Archimèdès discrète (petits points et tirets verts), à partir du losange rouge de coordonnées (0,6 ; 0,02342). La fonction j(a) et le gradient des fonctions de subénergie ont été évalués sur les points bleu clair. Les points rouges sont les minima locaux détectés par le TRUST. Le dernier (encerclé) est une première estimation du MG. Le vrai MG, le minimum secondaire et le point de selle sont symbolisés respectivement par la grande croix, la petite croix et l’étoile bleues.
Figure 34. Principe de la minimisation de la fonction coût J(p) par le recuit simulé. Les détails sont donnés dans le texte.
Figure 35. Principe de la minimisation par l’algorithme génétique. Les détails sont donnés dans le texte.
Figure 36. Evolution du coût au cours de l’estimation de Kdes et Kag (a) par le TRUST: le coût des vecteurs évalués est représenté par les points verts. Les six points rouges sont les estimations du MG calculées au cours de six minimisations successives. Le point vert encerclé montre que l’estimation de la première minimisation n’est pas optimale; (b) par le recuit simulé: les points rouges représentent le coût du dernier vecteur accepté à la fin de chaque seuil de recuit. Les points verts symbolisent les coûts les plus faibles et les plus élevés pour chaque seuil; (c) par l’algorithme génétique: les points rouges et verts indiquent respectivement le coût des individus les plus et les moins performants de chaque génération.
Figure 37. Minimisation de la section bidimensionnelle du coût par le recuit simulé. Le losange rouge symbolise le point de départ de coordonnées (0,6; 0,04684). Les petits points verts sont les 21 627 vecteurs évalués. Les points bleus sont les derniers vecteurs évalués à la fin de chacun des 156 seuils de recuit. La minimisation s’est arrêtée sur le point rouge. Le MG, le minimum secondaire et le point de selle sont symbolisés respectivement par la grande croix, la petite croix et l’étoile bleues.
Figure 38. Première minimisation de la section bidimensionnelle du coût par l’algorithme génétique. L’algorithme a évalué 1000 vecteurs de paramètres (petits points verts). La première génération de 5 individus est indiquée par les losanges verts. Les points bleus représentent les meilleurs individus de chacune des 200 générations. Le point rouge est la première estimation du MG. Le MG, le minimum secondaire et le point de selle sont symbolisés respectivement par la grande croix, la petite croix et l’étoile bleues.
Figure 39. Estimation des huit paramètres du modèle utilisés pour calculer les pseudo-données décrites dans la section 4.2.2(b). (a) Evolution du coût pendant la minimisation par le recuit simulé. Pour chaque seuil de recuit, les points verts représentent les coûts extrêmes, et les points rouges le dernier coût évalué à la fin du seuil. (b) Evolution du coût lors de la minimisation par l’algorithme génétique sur 200 générations, puis par l’algorithme du gradient conjugué non-linéaire sur 16 itérations. Les points rouges et verts correspondent respectivement aux individus les plus et les moins performants de chaque génération. (c) Estimation des paramètres par l’algorithme génétique couplé à l’algorithme du gradient conjugué non-linéaire. Pour chaque paramètre, la différence entre la valeur estimée (pi) et la valeur optimale (piopt) est normalisée relativement à la valeur optimale.
Figure 40. Cube associé à un schème de dimension 3. Le schème **0 désigne la base du cube (d’après Man et al., 1997).
Figure 41. Illustration du critère de sélection des vecteurs de paramètres: tous ceux (tels que p1 et p2) dont les simulations de la variable d’état X(t) passent par les barres d’erreur des mesures les expliquent correctement. Ils sont dits acceptables.
Figure 42. Structure du domaine acceptable: il peut être formé de plusieurs bassins disjoints dont le contour peut être convexe ou concave (Mazzega, 2000). Les vecteurs appartenant aux bassins Dp1 et Dp2 sont des solutions inverses équivalentes vis-à-vis des erreurs sur les données.
Figure 43. Données in situ utilisées pour estimer les paramètres contrôlant le transfert de l’Al dans la colonne d’eau au site O. Les flux de masse (a) et d’Al (b) ont été mesurés au site O (Bory et Newton, 2000). Le profil d’Al particulaire mesuré au site O (c; Tachikawa et al., 1999) a été extrapolé après l’analyse des profils réalisés au site M et aux stations Harmattan les plus éloignées de la côte africaine (stations 8, 10 et 15 de la Figure 44; Copin-Montégut et Copin-Montégut, 1983). Le profil d’Al dissous (d) a été mesuré à la station IOC n°5 (Measures, 1995).
Figure 44. Localisation des stations à partir desquelles la base de données contraignant les flux d’Al au site O a été constituée. Les ronds et les triangles rouges représentent respectivement les stations EUMELI et Harmattan, dont les numéros de stations sont indiqués (Copin-Montégut et Copin-Montégut, 1983). Le carré rouge localise la station IOC n°5. CC: Courant des Canaries; NASG: Gyre Subtropicale Nord Atlantique; NECC: Contre-Courant Nord Equatorial; NEC: Courant Nord Equatorial; MU: Upwelling Mauritanien.
Figure 45. Représentation des solutions acceptables trouvées lors des exps. A, B2, C, D et E (Tableau 17). Au cours de chaque expérience (délimitée par les traits épais verticaux noirs), dès que l’AG détecte un nouveau vecteur de paramètres acceptables, ses 8 composantes sont reportées par un rond coloré sur une verticale, immédiatement à droite du vecteur précédent. Pour chaque paramètre, l’axe des ordonnées correspond à l’intervalle de ses valeurs possibles (Tableau 18). Les simulations générées par les solutions indiquées par 8 étoiles dans les panneaux des exps. A et B2 sont représentées sur les figures 46 et 50 respectivement. Pour l’exp. C, les 4 solutions désignées par des étoiles sont, de gauche à droite, les solutions C1, C2, C3 et C4 (Tableaux 18 et 20). La solution C1 génère les simulations représentées sur la Figure 52. Les 8 lignes tiretées noires servent à comparer la solution C1 à celles trouvées au cours des exps. D et E (Tableau 17).
Figure 46. Flux de masse (a), d’Al (b), Al particulaire (c) et dissous (d) simulés par le vecteur de paramètres acceptables trouvé lors de l’exp. A (Tableau 17) et indiqué par 8 étoiles vertes sur la Figure 45. Les simulations sont comparées aux mesures des pièges à particules (a-b) qui ont été assimilées et aux profils calculés des phases filtrée et dissoute, qui n’ont pas été assimilés. Les profils simulés de Cpe et Cde sont d’autant plus récents qu’ils sont sombres.
Figure 47. Flux de masse (a), d’Al (b), Al particulaire (c) et dissous (d) simulés par l’un des vecteurs de paramètres acceptables trouvé lors de l’inversion simulée B1 (Tableau 17; Figure 48). Les simulations sont comparées aux pseudo-données calculées par COLDO avec le vecteur de paramètres indiqué dans le Tableau 18. Les profils simulés de Cpe et Cde sont d’autant plus récents qu’ils sont sombres.
Figure 48. Représentation des solutions acceptables au fur et à mesure de leur détection par l’AG lors de l’inversion simulée B1 (Tableau 17). Leurs composantes sont reportées par 8 points rouges sur une verticale dans le cadran correspondant à chaque paramètre, dont les gammes de valeurs possibles sont indiquées sur l’axe des ordonnées. Les 8 étoiles noires désignent le vecteur utilisé pour calculer les simulations de la Figure 47. Les 8 lignes noires tiretées désignent les paramètres utilisés pour calculer le jeu de pseudo-données (Tableau 18).
Figure 49. Coupe de la fonction coût associée aux pseudo-données calculées pour l’inversion simulée B1 (Tableau 17) en fonction de Krg et Vg. Les valeurs des autres paramètres sont égales aux valeurs optimales (Tableau 18). La ligne noire épaisse localise l’isocontour J(p) = 1. La croix et l’étoile bleues illustrent la migration du Minimum Global (MG) dûe au bruit ajouté aux pseudo-données.
Figure 50. Flux de masse (a), d’Al (b), Al particulaire (c) et dissous (d) simulés par le vecteur de paramètres acceptables trouvé lors de l’exp. B2 (Tableau 17), et indiqué par 8 étoiles bleues sur la Figure 45. Ils sont comparés aux mesures des pièges à particules et aux profils calculés pour les phases filtrée et dissoute qui ont tous été assimilés. Les profils simulés de Cpe et Cde sont d’autant plus récents qu’ils sont sombres.
Figure 51. Représentation des rapports Kdes/Kag’, Krp/Krg, Krp/Kad et Vg/Vp associés aux solutions acceptables des exps. B2, C, D et E (Tableau 17; Figure 45). Le mode de représentation est le même que pour la Figure 45: pour chaque expérience (délimitée par les traits épais verticaux noirs), à chaque fois que l’AG détecte une nouvelle solution acceptable, les 4 ou 5 rapports qui lui sont associés sont reportés par autant de ronds sur une verticale, dans le cadran qui leur correspond. Le paramètre Kag’ n’a pas été défini pour l’exp. B2. Les valeurs extrêmes des rapports associées à chaque expérience sont reportées dans le Tableau 19. La solution de l’exp. B2 désignée par les étoiles bleues génère les simulations de la Figure 50. Les quatre solutions de l’exp. C désignées par des étoiles rouges sont, de gauche à droite, les solutions C1, C2, C3 et C4 (Tableau 20).
Figure 52. Flux de masse (a), d’Al (b), Al particulaire (c) et dissous (d) simulés par la solution acceptable C1 trouvée lors de l’exp. C (Tableau 17), et indiquée par 8 étoiles rouges sur la Figure 45. Les simulations sont comparées aux mesures des pièges à particules et aux profils calculés pour les phases filtrée et dissoute qui ont tous été assimilés. Les profils simulés de Cpe et Cde sont d’autant plus récents qu’ils sont sombres.
Figure 53. Distribution de l’Al dans 1 m3 d’eau de mer à 2500 m au site EUMELI oligotrophe le 1er décembre 1991 calculée par les solutions C1 (a), C3 (b), et C4 (c). Les quantités d’Al échangées entre les phases au cours de dt = 1 j sont indiquées en rouge. Celles qui sont échangées avec la colonne d’eau sous- ou sus-jacente par mélange vertical pendant dt = 1 j sont indiquées en bleu. Enfin, les quantités d’Al particulaire qui ont traversé le volume de 1 m3 pendant cette même durée sont indiquées en marron. Pour la clarté des schémas, les grandeurs sont fournies avec deux chiffres significatifs. Les paramètres associés à chaque solution sont donnés dans le Tableau 20.
Figure 54. Contributions des termes de la nouvelle version de COLDO (Eqs. 25 et 3 à 5) à la variabilité temporelle de Fm, Fe, Cpe et Cde à 2500 m calculées par la solution C1 (Figures 45 et 51 ; Tableau 20).
Figure 55. Contributions des termes de la nouvelle version de COLDO (Eqs. 25 et 3 à 5) à la variabilité temporelle de Fm, Fe, Cpe et Cde à 2500 m calculées par la solution C3 (Figures 45 et 51 ; Tableau 20).
Figure 56. Contributions des termes de la nouvelle version de COLDO (Eqs. 25 et 3 à 5) à la variabilité temporelle de Fm, Fe, Cpe et Cde à 2500 m calculées par la solution C4 (Figures 45 et 51 ; Tableau 20).
Figure 57. Flux de masse (a), d’Al (b), Al particulaire (c) et dissous (d) simulés par la solution acceptable C2 trouvée lors de l’exp. C (section 8.2.2; Tableau 20). Les simulations sont comparées aux mesures des pièges à particules et aux profils calculés pour les phases filtrée et dissoute qui ont tous été assimilés. Les profils simulés de Cpe et Cde sont d’autant plus récents qu’ils sont sombres.
Figure 58. Profils des flux de masse (a) et d’Al (b) simulés à partir de la solution C2 (Figure 45 ; Tableau 20). Ils montrent des structures verticales de petite échelle (~ 100 m). Elles ne sont pas observables à partir des pièges à particules, mais il serait possible de vérifier leur existence à des profondeurs inférieures à 1000 m à partir du profileur vidéo sous-marin (section 2.2.2(d)).
Figure 59. Données in situ utilisées pour estimer les paramètres contrôlant le transfert du Corg dans la colonne d’eau au site O. Les flux de masse (a) et de COP (b) ont été mesurés au site O (Legeleux et al., 1996; Khripounoff et al., 1998; Bory et al., 2001). Les profils de COP filtré ont été réalisés pendant la campagne Harmattan (stations 8, 10 et 15, cf. Figure 44; Copin-Montégut et Copin-Montégut, 1983). Les profils de COD ont été mesurés au site O aux dates indiquées dans le Tableau 8 (Avril, 1995).
Figure 60. Solutions acceptables obtenues par l’assimilation des bases de données d’Al (exp. C), de Corg et de Ba au site O. Le mode de représentation est identique à celui de la Figure 45. La solution obtenue pour l’Al désignée par les étoiles rouges est la solution C1 (Tableau 20, Figure 52). Les paramètres de la solution obtenue pour le Corg et désignée par les étoiles bleues (solution Corg_O) sont indiqués dans le Tableau 21. Les simulations qu’elle génère sont représentées sur les figures 61 à 63. Les paramètres du vecteur Ba_O choisi pour le Ba et désigné par les étoiles vertes sont reportées dans le Tableau 23. Les simulations qu’il produit sont représentées sur les figures 66 à 68.
Figure 61. Flux de masse (a), de COP (b), COP filtré (c) et dissous (d) simulés par la solution Corg_O (Figure 60, Tableau 21). Les simulations sont comparées à la base de données constituée pour contraindre le Corg au site O (section 11.1.1). Les profils de Cpe et Cde sont d’autant plus récents qu’ils sont sombres.
Figure 62. Contributions des termes de la nouvelle version de COLDO (Eqs. 25 et 3 à 5) à la variabilité temporelle de Fm, Fe, Cpe et Cde à 2500 m calculées par la solution Corg_O (Tableau 21, Figure 60).
Figure 63. Distribution du Corg dans 1 m3 d’eau de mer à 2500 m au site EUMELI oligotrophe le 1er décembre 1991 calculée par la solution Corg_O (Figure 60, Tableau 21). Les quantités de Corg échangées entre les phases au cours de dt = 1 j sont indiquées en rouge. Celles qui sont échangées avec la colonne d’eau sous- ou sus-jacente par mélange vertical pendant dt = 1 j sont indiquées en bleu. Enfin, les quantités de COP qui ont traversé le volume de 1 m3 pendant cette même durée sont indiquées en marron.
Figure 64. Données in situ utilisées pour estimer les paramètres contrôlant les flux de Ba dans la colonne d’eau au site O. Les flux de masse (a) et de Ba (b) ont été mesurés au site O (Bory, 1997; Jeandel et al., 2000). Le profil de Ba particulaire filtré mesuré au site O (Tachikawa, 1997; Jeandel et al., 2000) a été extrapolé après analyse des profils réalisés pendant les programmes GEOSECS et MIDLANTE (Dehairs et al., 1980, cf. Figure 65). Les deux profils de Ba dissous ont été mesurés pendant les campagnes GEOSECS (Chan et al., 1977, cf. Figure 65).
Figure 65. Localisation des stations où ont été collectées les données in situ utilisées pour estimer les paramètres contrôlant les flux de Ba au site O (Figure 64). Les ronds, les trianges et les carrés rouges désignent respectivement les stations EUMELI, MIDLANTE (Dehairs et al., 1980) et GEOSECS (Chan et al., 1977).
Figure 66. Flux de masse (a), de Ba (b), Ba particulaire filtré (c) et dissous (d) simulés par le vecteur Ba_O (Figure 60, Tableau 23). Les simulations sont comparées à la base de données constituée pour contraindre le Ba au site O (section 11.2.1). Les profils de Cpe et Cde sont d’autant plus récents qu’ils sont sombres.
Figure 67. Contributions des termes de la nouvelle version de COLDO (Eqs. 25 et 3 à 5) à la variabilité temporelle de Fm, Fe, Cpe et Cde à 2500 m calculées par le vecteur Ba_O (Tableau 23, Figure 66).
Figure 68. Distribution du Ba dans 1 m3 d’eau de mer à 2500 m au site EUMELI oligotrophe le 1er décembre 1991 calculés par le vecteur Ba_O (Figure 60, Tableau 23). Les quantités de Ba échangées entre les phases au cours de dt = 1 j sont indiquées en rouge. Celles qui sont échangées avec la colonne d’eau sous- ou sus-jacente par mélange vertical pendant dt = 1 j sont indiquées en bleu. Enfin, les quantités de Ba particulaire qui ont traversé le volume de 1 m3 pendant cette même durée sont indiquées en marron
Figure 69. Données in situ utilisées pour estimer les paramètres contrôlant les flux d’Al dans la colonne d’eau au site M. Les flux de masse (a) et d’Al (b) ont été mesurés au site M (Legeleux et al., 1996; Bory, 1997; Bory et Newton, 2000). Le profil d’Al particulaire mesuré au site M (c; Tachikawa et al., 1999) a été interpolé puis extrapolé entre 1000 et 3100 m. Les profils d’Al particulaire filtré et de la concentration totale en particules filtrées mesurés pendant la campagne Guidome (c ; C. Copin, communication personnelle, 2000) sont utilisés pour estimer la concentration de l’Al dans ces particules. Le profil d’Al dissous (d) a été mesuré à la station IOC n°5 (Measures, 1995).
Figure 70. Localisation des stations où ont été collectées les données in situ utilisées pour estimer les paramètres contrôlant les flux d’Al et de Corg au site M (Figures 69 et 72). Les ronds, les losanges et le carré rouge désignent respectivement les stations EUMELI, Guidome (Copin-Montégut et Copin-Montégut, 1983) et IOC n°5 (Measures, 1995). CC: Courant des Canaries; NASG: Gyre Subtropicale Nord Atlantique; NECC: Contre-Courant Nord Equatorial; NEC: Courant Nord Equatorial; MU: Upwelling Mauritanien.
Figure 71. Flux de masse (a), d’Al (b), Al particulaire filtré (c) et dissous (d) simulés par le vecteur Al_M (Tableau 24). Les simulations sont comparées à la base de données constituée pour contraindre l’Al au site M (section 12.1.1). Les profils de Cpe et Cde sont d’autant plus récents qu’ils sont sombres.
Figure 72. Données in situ utilisées pour estimer les paramètres contrôlant les flux de Corg dans la colonne d’eau au site M. Les flux de masse (a) et de COP (b) ont été mesurés au site M (Legeleux et al., 1996; Bory et al., 2001). Les profils de COP filtré ont été réalisés pendant la campagne Guidome (Figure 70 ; Copin-Montégut et Copin-Montégut, 1983). Les profils de COD ont été réalisés au site M aux dates indiquées dans le Tableau 8 (Avril, 1995).
Figure 73. Solutions acceptables obtenues par l’assimilation des bases de données de Corg collectées au site O (points et étoiles bleues), au site M sur toute la durée de la campagne (points et étoiles turquoises) et au site M pendant le bloom de 1991 (points et étoiles vertes). Le mode de représentation est identique à celui de la Figure 45. Les paramètres des solution Corg_O (section 11.1.3(b)), Corg_M et Corg_Mb sont désignés respectivement par les étoiles bleues, turquoises et vertes. Leurs valeurs figurent dans le Tableau 25.
Figure 74. Flux de masse (a), de COP (b), COP filtré (c) et dissous (d) simulés par la solution Corg_M (Figure 73, Tableau 25). Les simulations sont comparées à la base de données constituée pour contraindre le Corg au site M (section 12.2.1). Les profils de Cpe et Cde sont d’autant plus récents qu’ils sont sombres.
Figure 75. Distribution du Corg dans 1 m3 d’eau de mer à 2500 m au site EUMELI mésotrophe le 1er décembre 1991 (période hors bloom) calculée par la solution Corg_M (Figure 73, Tableau 25). Les quantités de Corg échangées entre les phases au cours de dt = 1 j sont indiquées en rouge. Celles qui sont échangées avec la colonne d’eau sous- ou sus-jacente par mélange vertical pendant dt = 1 j sont indiquées en bleu. Enfin, les quantités de COP qui ont traversé le volume de 1 m3 pendant cette même durée sont indiquées en marron.
Figure 76. Contributions des termes de la nouvelle version de COLDO (Eqs. 25, 3 à 5) à la variabilité temporelle de Fm, Fe, Cpe et Cde à 2500 m calculées par la solution Corg_M (Figure 73, Tableau 25).
Figure 77. Flux de masse (a), de COP (b), COP filtré (c) et dissous (d) simulés par la solution Corg_Mb (Figure 73, Tableau 25). Les simulations sont comparées à la base de données constituée pour contraindre le Corg au site M (section 12.2.1) que l’on a assimilée entre le 13 février et le 2 août 1991. Les profils de Cpe et Cde sont d’autant plus récents qu’ils sont sombres.
Figure 78. Distribution du Corg dans 1 m3 d’eau de mer à 2500 m au site EUMELI mésotrophe pendant le bloom de 1991 (1er juin 1991) calculée par la solution Corg_Mb (Figure 73, Tableau 25). Les quantités de Corg échangées entre les phases au cours de dt = 1 j sont indiquées en rouge. Celles qui sont échangées avec la colonne d’eau sous- ou sus-jacente par mélange vertical pendant dt = 1 j sont indiquées en bleu. Enfin, les quantités de COP qui ont traversé le volume de 1 m3 pendant cette même durée sont indiquées en marron.
Figure 79. Contributions des termes de la nouvelle version de COLDO (Eqs. 25, 3 à 5) à la variabilité temporelle de Fm, Fe, Cpe et Cde à 2500 m pendant le bloom de l’année 1991 calculées par la solution Corg_Mb (Figure 73, Tableau 25).
Table des tableaux
Tableau 1. Couples radio-isotopiques utilisés pour la calibration des pièges in situ (Bacon, 1996). Entre parenthèses est indiqué le temps de demi-vie de l’élément fils.
Tableau 2. Caractéristiques des trois sites EUMELI (* : Morel et al., 1996)
Tableau 3. Principaux constituants de la matière particulaire échantillonnés dans la colonne d’eau à l’occasion du programme EUMELI
Tableau 4. Caractéristiques temporelles et spatiales des échantillons exploitables collectés par les pièges utilisés au site O
Tableau 5. Caractéristiques temporelles et spatiales des échantillons exploitables collectés par les pièges utilisés au site M.
Tableau 6. Echantillonnage de la phase en suspension aux sites EUMELI en juin 1992 (Tachikawa, 1997; Tachikawa et al., 1999). Les échantillons pouvant servir à l’étude de la colonne d’eau entre 1000 m et le fond sont indiqués en gras.
Tableau 7. Echantillonnage de la phase dissoute aux sites EUMELI (Tachikawa, 1997). Les échantillons pouvant servir à l’étude de la colonne d’eau sont indiqués en gras.
Tableau 8. Dates des mesures des profils de carbone organique dissous aux sites EUMELI (Avril, 1995).
Tableau 9. Flux de masse moyen et sa composition moyenne dans la colonne d’eau au site O (n.d. :absence de mesure). Les calculs ont été faits à partir des données collectées simultanément d’avril 1991 à avril 1992 (367 jours).
Tableau 10. Flux de masse moyen et sa composition moyenne dans la colonne d’eau au site M (n.d: absence de mesure; * : le calcul a été fait avec un nombre de données réduit, soit 88 jours de collecte uniquement)
Tableau 11. Définition des variables d’états et des paramètres du modèle COLDO (x est un élément ou une molécule chimique).
Tableau 12. Tableau récapitulatif de quelques caractéristiques du modèle COLDO.
Tableau 13. Valeurs des paramètres utilisées pour calculer les données artificielles associées aux cartes des figures 25 à 27.
Tableau 14. Compilation bibliographique des estimations des paramètres biogéochimiques du cycle des particules océaniques (Athias et al., 2000a). Ces travaux sont basés sur l’utilisation de modèles des échange dissous-particulaire similaires à COLDO, mais l’estimation des paramètres repose la plupart du temps sur l’hypothèse d’état stationnaire (cf. section 3.2.1(a)).
Tableau 15. Résultats des expériences d’inversions simulées. On rappelle que les pseudo-données fabriquées à partir du modèle sont non bruitées.
Tableau 16. Délimitation des intervalles de recherche des huit paramètres du modèle à partir d’une compilation bibliographique.
Tableau 17. Caractéristiques des expériences d’inversion présentées dans le Chapitre 8.
Tableau 18. Valeurs des paramètres du modèle COLDO mentionnées dans les expériences d’assimilation des données in situ décrivant le transfert de l’Al au site O (Tableau 17).
Tableau 19. Valeurs extrêmes de certains rapports de paramètres de COLDO délimités par les expériences d’inversion présentées dans le Chapitre 8 (Tableau 17). Etant donnée la nature éventuellement discontinue des domaines acceptables, ces intervalles peuvent eux-mêmes être discontinus. Les rapports associés à la solution C1 (Tableau 18) appartiennent aux intervalles délimités par les exps. D et E.
Tableau 20. Valeurs des paramètres pour quatre des solutions de l’exp. C (Tableau 17, Figures 45 et 51).
Tableau 21. Intervalles de recherche des paramètres de COLDO utilisés pour les expériences d’assimilation de la base de données de Corg au site O. La solution Corg_O est désignée par des étoiles bleues sur la Figure 60. Elle génère les simulations représentées sur la Figure 61.
Tableau 22. Constantes de dégradation du COP labile (k1) et peu labile (k2) fixé sur des particules prélevées en Mer Ligure. Elles ont été calculées par l’ajustement au sens des moindres carrés d’un modèle “ 2G” à des résultats d’expériences de dégradation in vitro (Sempéré et al., 2000).
Tableau 23. Intervalles de recherche des paramètres de COLDO utilisés pour les expériences d’assimilation de la base de données de Ba au site O. Le vecteur Ba_O est désigné par des étoiles vertes sur la Figure 60. Il génère les simulations représentées sur les figures 66 à 68.
Tableau 24. Limites de l’espace de recherche des paramètres expliquant la distribution de l’Al au site M. La solution C1 est celle que nous avons sélectionnée pour quantifier les flux d’Al au site O (section 9.2.1). Le vecteur Al_M est l’un des vecteurs évalués par l’AG lors de l’assimilation de la base des données d’Al au site M. Il génère les simulations représentées sur la Figure 71.
Tableau 25. Limites de l’espace de recherche des paramètres expliquant la distribution du Corg au site M. La solution Corg_O est celle que nous avons sélectionnée pour quantifier les flux de Corg au site O (section 11.1.3(b)). La solution Corg_M est l’une des solutions acceptables identifiées par l’AG après assimilation de la base de données associée au site M sur toute la durée de la campagne (Figure 73). Elle génère les simulations représentées sur les figures 74 à 76. La solution Corg_Mb est l’une des solutions acceptables identifiées par l’AG après assimilation de la même base de données entre le 13 février et le 2 août 1991 (Figure 73). Elle génère les simulations représentées sur les figures 77 à 79.
Tableau 26. Inventaire des données rassemblées au site EUMELI oligotrophe
Tableau 27. Inventaire des données rassemblées au site EUMELI mésotrophe
Tableau 28. Inventaire des données collectées au site EUMELI eutrophe
Table des abbréviations
Abbréviation | Signification |
AABW | Antarctique Bottom Water |
AG | Algorithme Génétique |
AOG | Algorithme d’Optimisation Globale |
CC | Canaries Current |
CID | Carbone Inorganique Dissous |
COP | Carbone Organique Particulaire |
COD | Carbone Organique Dissous |
Corg | Carbone organique |
CVFZ | Cape Verde Frontal Zone |
EDO | Equation aux Dérivées Ordinaires |
EDP | Equation aux Dérivées Partielles |
EDPNLC | Equation aux Dérivées Partielles Non-Linéaires Couplées |
EUC | Equatorial UnderCurrent |
GC | Gradient Conjugué |
GW | Guinea Water |
IOC | International Oceanographic Commission |
ITCZ | InterTropical Convergence Zone |
MOW | Mediterranean Outflow Water |
MG | Minimum Global |
MS | Minimum Secondaire |
MU | Mauritanian Upwelling |
NACW | North Atlantic Central Water |
NADW | North Atlantic Deep Water |
NASG | North Atlantic Subtropical Gyre |
NEC | North Equatorial Current |
NECC | North Equatorial Counter Current |
PS | Point de Selle |
PFP | Plus Forte Pente |
RS | Recuit Simulé |
SACW | South Atlantic Central Water |
SAIW | South Atlantic Intermediate Water |
site E | site EUMELI eutrophe |
site M | site EUMELI mésotrophe |
site O | site EUMELI oligotrophe |
SW | Surface Water |
TRUST | Terminal Repeller Unconstrained Subenergy Tunneling |
Face à l’augmentation de la concentration des gaz à effet de serre, la communauté scientifique internationale accorde un intérêt croissant à l’étude des cycles biogéochimiques. Ces cycles correspondent aux échanges de matière et d’énergie entre les continents, l’atmosphère, l’océan, et - à l’échelle des temps géologiques - les couches internes de la planète. Ils concernent à la fois le monde vivant et le monde minéral. Le dioxyde de carbone (CO2) est le principal responsable de l’effet de serre naturel. L’accroissement de sa concentration dans l’atmosphère lié aux seules activités humaines (industrie, chauffage, transport, mise à feu des forêts équatoriales) correspond aux trois quarts de sa variation naturelle entre un âge glaciaire et un âge interglaciaire. L’océan est avec la biosphère continentale l’un des puits majeurs du CO2 (Quay et al., 1992) : il absorberait environ un tiers des émissions anthropiques (Siegenthaler et Sarmiento, 1993). Ainsi, comprendre et quantifier les mécanismes océaniques responsables du piégeage du CO2 sont devenus les objectifs majeurs de grands programmes internationaux tels que JGOFS (Joint Global Ocean Flux Study ; JGOFS, 1987).
Dans l’océan, le principal réservoir de carbone est le Carbone Inorganique Dissous (CID). Celui-ci se présente principalement sous forme de bicarbonates (HCO3-, à ~89 %), de carbonates (CO32-, à ~10 %) et de CO2 dissous (à ~1 %). Ces trois espèces chimiques sont reliées entre elles par l’équilibre des carbonates, le CO2 dissous étant en équilibre avec le CO2 atmosphérique (Copin-Montégut, 1989). L’abondance des trois formes du CID et par conséquent les échanges de CO2 à l’interface air/mer varient en fonction de l’évaporation, des précipitations et des apports d’eau douce vers l’océan. Ils dépendent également de la température et de la pression partielle du CO2 atmosphérique. Enfin, ils sont fortement influencés par l’activité biologique. Par le biais de la photosynthèse, les communautés phytoplanctoniques vivant dans les eaux de surface de l’océan incorporent du carbone dans leurs tissus organiques. Certaines espèces synthétisent des tests de carbonate de calcium (CaCO3). Ces deux mécanismes déplacent l’équilibre chimique entre les différentes formes du CID. Les déchets des organismes planctoniques (cadavres, mues, tests, exsudats, pelotes fécales) sont ensuite partiellement dégradés et recyclés dans la couche de surface par l’activité d’organismes hétérotrophes tels que le zooplancton et les bactéries. Une fraction de cette matière est compactée en de gros agrégats (Cowen et Holloway, 1996) qui sédimentent vers le fond de l’océan. Au cours de leur chute, ils subissent une dégradation partielle qui permet la redistribution des éléments chimiques qui les composent. Il s’agit des principaux éléments constitutifs de la matière organique (carbone, mais également azote, phosphore et soufre), des éléments qui composent les tests ou exosquelettes planctoniques (calcium, silice), ainsi que d’éléments présents en trace dans l’océan (aluminium, baryum, cadmium, nickel, zinc…). La fraction non dégradée est progressivement enfouie dans les sédiments. Ce flux de particules jouerait un rôle important dans le piégeage océanique du CO2 (Alldredge et Jackson, 1995) : ce mécanisme constitue ce qu’on appelle la pompe biologique. Ce flux intervient également dans le contrôle de la composition chimique de l’eau de mer. Ce sont les raisons pour lesquelles nous nous proposons de l’étudier dans cette thèse.
Les particules océaniques ne sont pas toutes “ authigènes” , c’est-à-dire produites in situ dans l’océan. Certaines sont apportées par les fleuves et par l’atmosphère (Lal, 1977). Les apports fluviaux sont essentiellement répartis à proximité des embouchures. Par contre, l’atmosphère représente une source majeure de particules minérales produites par l’érosion éolienne des régions arides et semi-arides de la Terre (Prospero, 1996). A la différence des particules biogéniques, les poussières minérales sont principalement réfractaires, mais une partie des éléments qui les composent sont solubles dans l’eau de mer (Jickells, 1995 ; Kubilay et Saydam, 1995 ; Medinets, 1996). Elles sont également responsables de l’adsorption d’éléments dissous. Les particules minérales ont donc elles aussi un impact sur la composition chimique de l’eau de mer. En enrichissant les eaux de surface en nutriments (phosphore, fer), elles influenceraient directement l’activité biologique (Martin et al., 1994; Herut et Krom, 1996 ). Elles pourraient accroître l’efficacité de la pompe biologique, en augmentant la densité des particules biogéniques dans lesquelles elles se trouvent incorporées (Donaghay et al., 1991) et en protégeant la matière organique de la dégradation bactérienne.
L’enfouissement du CO2 atmosphérique en excès et la composition de l’eau de mer dépendent donc en partie du devenir des particules dans la colonne d’eau océanique. Il est contrôlé par un ensemble de mécanismes complexes et fortement couplés, de nature à la fois physique, chimique et biologique. Du point de vue physique, les courants advectifs et turbulents peuvent induire l’agrégation et la désagrégation des particules (Ruiz, 1996). L’efficacité de la coagulation est très dépendante de la nature physique et chimique de la surface des particules, qui est quant à elle contrôlée par des processus biologiques (Riebesell, 1991; Jackson et Lochmann, 1993; Engel et Schartau, 1999). Les réactions chimiques de désorption, dissolution, adsorption (Balistrieri et al., 1981; Honeyman et al., 1988) et précipitation interviennent dans les échanges entre les phases dissoute et particulaire. Les échanges dissous-particulaire résultent également de mécanismes biologiques. Par exemple, le phytoplancton absorbe activement des sels nutritifs (Jacques et Tréguer, 1986) et des métaux en trace (Fisher et Reinfelder, 1995) sous forme dissoute pour sa croissance. D’autre part, les plus gros agrégats abritent des communautés microbiennes et servent de refuge à des protozoaires ainsi qu’à du microzooplancton (Alldredge et Silver, 1988; Alldredge et Gotschalk, 1990). Les bactéries fixées sur les particules et celles qui sont libres dans l’eau de mer sont responsables d’une partie de la dégradation des particules (Biddanda et Pomeroy, 1988; Cho et Azam, 1988; Simon et al., 1990; Smith et al., 1992). Le zooplancton, et en particulier les copépodes, induisent également une transformation des particules lorsqu’ils les broutent puis libèrent des déchets sous forme de pelotes fécales (Carlotti et Radach, 1996; Cowie et Hedges, 1996). L’ensemble de ces mécanismes co- et inter-agissent à toutes les échelles temporelles et spatiales, de façon variable selon les apports atmosphériques comme nous l’avons mentionné ci-dessus, et selon l’environnement physique et biologique local (Wassman, 1998). En effet, les réseaux trophiques qui se développent dans des eaux où les nutriments sont abondants sont très productifs et exportent sous forme de gros agrégats une partie importante de la matière organique qu’ils produisent. Par contre, ceux qui se développent dans des zones carencées en nutriments vont se maintenir en recyclant la matière organique produite et en minimisant son exportation.
Mesurer les flux de carbone dans l’océan et la distribution du carbone entre les phase dissoute et particulaire ne permet pas directement de comparer quantitativement l’importance de ces processus car le carbone organique est un composé très labile (Bianchi et al., 1998; Sempéré et al., 2000). Pour quantifier des mécanismes précis, les géochimistes utilisent une palette d’outils ou traceurs. Il s’agit essentiellement d’éléments chimiques et de molécules dont la distribution, du fait de leur réactivité spécifique, reflète l’importance d’un processus. En voici quelques exemples. Les isotopes du thorium (Th) tels que le 230Th et le 234Th sont peu solubles, et par conséquent rapidement piégés par les particules marines. Cela induit dans l’eau de mer un déséquilibre radioactif entre ces isotopes et leurs pères respectifs (234U et 238U) au contraire très solubles. La mesure de ce déséquilibre est fréquemment utilisée pour étudier les interactions entre les phases dissoute et particulaire (Bacon et Anderson, 1982; Baskaran et al., 1992, 1996; Roy-Barman et al., 1996) et les processus d’agrégation et de désagrégation des particules (Bacon et al., 1985; Nozaki et al., 1987; Cochran et al., 1993). En raison de la quantité importante et relativement constante de l’aluminium dans les matériels d’origine crustale (7,1 à 7,4 % en masse ; Taylor, 1964), de sa faible solubilité dans l’eau des précipitations et dans l’eau de mer, cet élément est un traceur privilégié des apports atmosphériques d’origine continentale dans l’océan (Bory et Newton, 2000). Un ensemble de processus biologiques actifs et/ou passifs induisent la précipitation du baryum dissous en cristaux de barytine (Dehairs et al., 1980) dans les eaux superficielles de l’océan (Legeleux et Reyss, 1996), cela malgré la sous-saturation de l’eau de mer par rapport à la barytine (Monnin et al., 1999). La mesure du flux de barytine dans l’océan permet de quantifier la productivité des écosystèmes actuels et passés (Jeandel et al., 1995; Dymond et Collier, 1996; François et al., 1997). Les isotopes stables du plomb (206Pb, 207Pb et 208Pb) et leurs rapports isotopiques servent à identifier les sources de plomb anthropique et à étudier le transfert de ce terme anthropique dans l’océan (Hamelin et al., 1997; Alleman et al., 1999). Enfin, les isotopes du néodyme (143Nd et 144Nd) et la concentration des terres rares sont utilisés pour caractériser les sources de matière vers l’océan (Tachikawa et al., 2001), identifier les trajectoires des masses d’eau (Piepgras et Wasserburg, 1987; Jeandel, 1993; Jeandel et al., 1998; Lacan et Jeandel, 2001) et étudier les interactions entre particules, comme entre les phases dissoute et particulaire (Jeandel et al., 1995 ; Tachikawa et al., 1997, 1999).
En parallèle aux études focalisées sur des mécanismes précis, des travaux ont été consacrés à la formalisation de modèles numériques simulant les échanges entre les phases dissoute et particulaire à l’échelle de la colonne d’eau océanique. La modélisation est une approche extrêmement fructueuse pour étudier les systèmes complexes (Coquillard et Hill, 1997). Construire un modèle exige en effet de synthétiser la somme des connaissances accessibles à un instant donné sur un système, et de sélectionner judicieusement les faits importants dans le temps et dans l’espace pour décrire un phénomène intéressant. Cela revient à fabriquer une image simplifiée et plus maniable de la réalité brute. Bien entendu, un modèle n’est pas destiné à survivre indéfiniment. De nouvelles expériences ou observations vont mettre en évidence certains défauts, et conduire à proposer un nouveau modèle. La modélisation conduit ainsi à une alternance permanente de mises au point et de remises en cause de connaissances : il s’agit là du processus même de l’avancement de la science.
La modélisation des échanges dissous-particulaire dans la colonne d’eau océanique a débuté dans les années 1970 (Craig, 1974). Elle est fondée sur des modèles à compartiments représentant les phases dissoute et particulaire. Chaque terme d’échange entre deux compartiments intègre l’effet résultant de tout un ensemble de mécanismes de nature et d’échelles temporelle et spatiale variées, telles que ceux que nous avons mentionnés plus haut. Les échanges sont décrits par des fonctions mathématiques très simples incluant des constantes de temps que l’on appelle les paramètres du modèle. Quantifier les processus qui expliquent les observations du transfert du carbone et des éléments associés dans la colonne d’eau revient à calculer les paramètres avec lesquels le modèle développé fournit les simulations qui se rapprochent le plus de ces observations. Ce calcul correspond à l’inversion du modèle.
On appelle méthode inverse toute méthode combinant des observations et un modèle théorique d’un phénomène observé. Les objectifs sont variés : estimation paramétrique, interpolation entre des observations (McIntosh, 1990), reconstitution des forçages du système, configuration de systèmes d’observation (Barth et Wunsch, 1990 ; Barth, 1992; Hernandez et al., 1995)… Les méthodes inverses qui nous intéressent plus particulièrement ont d’abord été développées dans les domaines de la météorologie et de la géophysique (Tarantola, 1987; Menke, 1989), puis elles ont été appliquées à l’océanographie physique (Bennett, 1992; Wunsch, 1996). Elles reposent sur l’hypothèse que les processus sont localement linéaires, c’est-à-dire simplement proportionnels à l’une des variables du système. L’avantage des systèmes linéaires est qu’ils peuvent être décomposés en éléments simples puis reconstruits.
Mais en réalité les phénomènes naturels sont pour la grande majorité non-linéaires, c’est-à-dire qu’ils résultent de relations non proportionnelles entre les variables du système. Comme le notent Goldenfeld et Kadanoff (1999) : “ Every place we look – outside the physics classroom- we see a world of amazing complexity”note 1 .
Les systèmes biogéochimiques en particulier intègrent une complexité intrinsèque résultant d’interactions non-linéaires entre des processus de nature et d’échelles variées : ils ne peuvent donc pas être simplement décomposés en briques élémentaires puis reconstruits. Depuis les travaux du français H. Poincaré (1892; 1893; 1899) sur les systèmes dynamiques on sait que les modèles non-linéaires peuvent adopter des comportements dynamiques complexes, sensibles aux fonctions mathématiques utilisées pour décrire les processus, aux conditions initiales des simulations et à la valeur des paramètres, et cela même si les équations paraissent être sommaires (May, 1976).
Au commencement de ma thèse en 1997, nous soupçonnions que l’inversion d’un modèle biogéochimique non-linéaire même simple, tel qu’un modèle des échanges dissous-particulaire dans la colonne d’eau océanique, allait faire surgir des difficultés pour lesquelles les méthodes inverses classiques, linéaires, n’ont pas été conçues. Pourtant plusieurs travaux avaient déjà été publiés sur l’inversion de modèles non-linéaires d’écosystèmes planctoniques (Vézina et Platt, 1988; Fasham et Evans, 1995; Murnane et al., 1996; Prunet et al., 1996b). Ils ne présentent pas de véritable analyse de la nature du problème mathématique sous-jacent et les méthodes utilisées reposent sur la théorie inverse linéaire. Il faut reconnaître que les outils mathématiques pour étudier les systèmes non-linéaires sont rares et parfois théoriquement complexes.
En plus d’une méthode inverse appropriée, l’inversion d’un modèle exige de disposer d’observations de terrain suffisamment nombreuses relativement au problème posé, et de bonne qualité. Or l’échantillonnage in situ de la biogéochimie de l’océan pose de nombreuses difficultés. Dans ce domaine, l’utilisation d’instruments satellites à haute couverture spatiale et temporelle est limitée à la mesure de la biomasse phytoplanctonique dans les eaux de surface (Antoine et al., 1996). L’échantillonnage de la colonne d’eau profonde exige d’organiser des campagnes en mer. Celles-ci demandent d’importants moyens financiers et humains, et sont soumises aux conditions météorologiques. Obtenir des mesures précises est une tâche délicate : les particules sont peu abondantes et la concentration dans la phase dissoute de la plupart des traceurs est très faible. La faible couverture, la faible résolution temporelle et spatiale des données et l’importance des erreurs de mesure sont des difficultés supplémentaires que nous devons prendre en compte.
L’objectif de cette thèse est, à partir d’un modèle et d’une base de données appropriés, de quantifier les processus de la colonne d’eau profonde associés aux flux de particules et d’analyser leur variabilité en réponse à celle de la productivité des eaux de surface et des apport atmosphériques.
Pour atteindre cet objectif, il est nécessaire :
Pour cela, une approche interdisciplinaire est indispensable. Ainsi, nous sommes allés fureter dans le domaine des mathématiques appliquées, et dans différentes disciplines concernées par la modélisation des systèmes complexes : optique non-linéaire (Carroll, 1996), électronique (Lecouvé et al., 2000), chimie (Banga et Seider, 1996), biotechnologies (Banga et al., 1997), médecine (Yang et al., 1998), intelligence artificielle (Michalewicz et al., 1996; Ratle et Sebag, 2000).
Pour constituer la base de données, nous avons choisi de rassembler les données collectées et les travaux publiés sur la colonne d’eau profonde à l’occasion du programme national EUMELI (1988-1992) organisé dans le cadre de la participation française au programme JGOFS. Son objectif était l’étude des principaux processus contrôlant les flux de particules, depuis leur formation dans les eaux de surface jusqu’à leur enfouissement dans le sédiment (Morel, 1996, 2000). Pour cela, trois stations ont été échantillonnées dans la région de l’upwelling mauritanien, à environ 20°N, et à 200, 400 et 1400 km de la côte africaine (Figure 8). Cette disposition est particulièrement bien adaptée au problème géochimique posé, dans la mesure où on observe de la côte vers le large une nette diminution de la productivité des eaux de surface et du flux de poussières sahariennes.
Le travail présenté dans ce manuscrit s’articule en quatre parties. La première partie débute par une présentation générale des flux de matière dans l’océan. Nous décrirons ensuite les techniques de mesure in situ de ces flux, avant de détailler la stratégie employée dans le cadre du programme EUMELI. Les techniques de mesure déterminent les hypothèses de modélisation, et le degré de simplification du modèle. Nous présenterons les caractéristiques du modèle choisi, en insistant sur ses propriétés dynamiques. La seconde partie est consacrée à l’identification d’une méthode inverse pour estimer les paramètres du modèle. Il s’agit dans un premier temps de déterminer la nature du problème mathématique à résoudre. Après avoir démontré l’inadéquation de l’approche inverse linéaire, nous analyserons les performances et le comportement de trois algorithmes dits d’optimisation globale en nous basant sur des expériences d’inversions simulées. Elles reposent sur l’utilisation d’observations artificielles non bruitées fabriquées à partir du modèle avec des paramètres connus que les algorithmes doivent être capables de retrouver. Nous sélectionnerons l’algorithme qui se révèle être le plus performant. La troisième partie consiste à tester et à terminer la mise au point de la méthode inverse en l’appliquant à un premier jeu de données in situ. Nous montrerons comment les fortes incertitudes sur les données compliquent la résolution du problème inverse. Cela nous conduira à envisager des améliorations de la méthode inverse et à proposer de nouvelles stratégies d’échantillonnage de la colonne d’eau. La quatrième partie débute par la sélection de trois traceurs des flux de matière océanique en fonction de leur intérêt géochimique et de la quantité de données disponibles pour décrire leur distribution dans la colonne d’eau aux sites EUMELI. Puis nous présenterons les résultats des expériences d’assimilation de ces données. Nous les comparerons à des résultats d’expériences in vitro et aux travaux publiés antérieurement sur les campagnes EUMELI. Enfin, nous récapitulerons les informations apportées par l’approche développée dans cette thèse sur le fonctionnement de la colonne d’eau.
Ce travail a été financé par l’Institut National des Sciences de l’Univers (INSU) dans le cadre :
